题目内容
如图所示，某同学在地面上拉着一个质量为m=30kg的箱子匀速前进，已知箱与地面间的动摩擦因数为μ=0.5，拉力F1与水平面夹角为θ=45°，g=10m/s2．求：
（1）箱子对地面的压力多大？
（2）绳子的拉力F1为多少？
分析：（1）对箱子受力分析，受拉力、重力支持力和摩擦力，根据平衡条件列方程求解即可．
（2）由第一问的解答可以得到第二问结果．
（2）由第一问的解答可以得到第二问结果．
解答：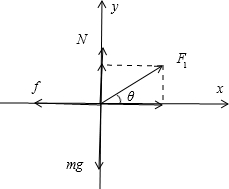
解：对箱子受力分析，如图
根据平衡条件，有
x方向：F1cos45°-f=0
y方向：N+F1sin45°-mg=0
其中：f=μN
解得
F1cos45°=μ（mg-F1sin45°）；
F1=
=100
N
N=200N
根据牛顿第三定律，箱子对地的压力等于地面对箱子的支持力；
故箱子对地面的压力为200N．
（2）由第一问解得，F1=100
N；
故绳子的拉力F1为100
N．
解：对箱子受力分析，如图根据平衡条件，有
x方向：F1cos45°-f=0
y方向：N+F1sin45°-mg=0
其中：f=μN
解得
F1cos45°=μ（mg-F1sin45°）；
F1=
| μmg |
| cos45°+μsin45° |
| 2 |
N=200N
根据牛顿第三定律，箱子对地的压力等于地面对箱子的支持力；
故箱子对地面的压力为200N．
（2）由第一问解得，F1=100
| 2 |
故绳子的拉力F1为100
| 2 |
点评：本题关键是对物体受力分析，然后根据共点力平衡条件并运用正交分解法列平衡方程求解．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，某同学在地面上拉着一个质量为m=30kg的箱子匀速前进，已知箱与地面间的动摩擦因数为μ=0.5，拉力F1与地面水平夹角为θ=45°．g=10m/s2，求：
如图所示，某同学在地面上拉着一个质量为m=30kg的箱子以2m/s匀速前进，已知箱与地面间的动摩擦因数为μ=0.5，拉力F1与水平面夹角为θ=45°，g=10m/s2。求：
