题目内容

在倾角为的固定光滑斜面上有两个用轻弹簧相连接的物块A、B，它们的质量分别为、，弹簧劲度系数为k，C为一固定挡板，系统处于静止状态．现用一平行于斜面向上的恒力F拉物块A使之向上运动，当物块B刚要离开挡板C时，物块A运动的距离为d，速度为，则此时

A．拉力做功的瞬时功率为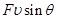
B．物块B的质量满足
C．物块A的加速度为
D．弹簧弹性势能的增量为

CD

解析试题分析：初始系统处于静止，弹簧处于压缩状态，根据A平衡得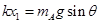，出现恒力F之后，当B刚要离开挡板时，挡板对B没有弹力，分析B可得弹簧处于拉伸，弹力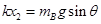。那么此过程中A运动的距离为，所以答案B中是错误的。物体A的加速度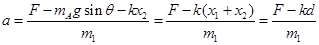答案C对。对A分析根据动能定理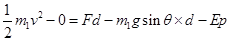整理得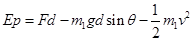答案D正确。此时拉力F的瞬时功率等于力和在力的方向上的速度乘积即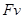答案A错。
考点：功功率 动能定理

练习册系列答案
相关题目

提高物体（例如汽车）运动速率的有效途径是增大发动机的功率和减小阻力因数（设阻力与物体运动速率的平方成正比，即Ff＝kv2，k是阻力因数）．当发动机的额定功率为P0时，物体运动的最大速率为vm，如果要使物体运动的速率增大到2vm，则下列办法可行的是

A．阻力因数不变，使发动机额定功率增大到2P0
B．发动机额定功率不变，使阻力因数减小到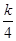
C．阻力因数不变，使发动机额定功率增大到8P0
D．发动机额定功率不变，使阻力因数减小到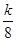

用大小相同的水平恒力分别沿着粗糙水平地面和光滑水平地面拉动原来处于静止的两个质量相同的物体移动相同一段距离，该过程中恒力的功和平均功率分别为W1、P1和W2、P2, 则两者关系是（       ）

A．W1＞W2、P1＞P2 B．W1=W2、P1＜P2
C．W1=W2、P1＞P2 D．W1＜W2、P1＜P2

如图所示，虚线框内存在匀强磁场，将正方形闭合导线框从如图所示的位置匀速拉出磁场，若第一次拉出时间为t，克服安培力做功为W1；第二次拉出时间为3t，克服安培力做功为W2，则:

A．W1=9W2B．W1=3W2
C．W1=W2D．

如图所示，水平传送带两端点A、B间的距离为L，传送带开始时处于静止状态。把一个小物体放到右端的A点，某人用恒定的水平力F使小物体以速度v1匀速滑到左端的B点，拉力F所做的功为W1、功率为P1，这一过程物体和传送带之间因摩擦而产生的热量为Q1。随后让传送带以v2的速度匀速运动,此人仍然用相同的水平力恒定F拉物体,使它以相对传送带为v1的速度匀速从A滑行到B，这一过程中, 拉力F所做的功为W2、功率为P2，物体和传送带之间因摩擦而产生的热量为Q2.下列关系中正确的是（     ）

A．W1＝W2 ,P1＜P2，Q1＝Q2
B．W1＝W2 ,P1＜P2，Q1＞Q2
C．W1＞W2 ,P1＝P2，Q1＞Q2
D．W1＞W2 ,P1＝P2，Q1＝Q2

如图所示，质量分别为m1和m2的两个物体，m1<m2，在大小相等的两个力F1和F2的作用下沿水平方向移动了相同的距离.若F1做的功为W1，F2做的功为W2，则(  ).
 

A．W1>W2B．W1<W2
C．W1=W2D．条件不足，无法确定

如图OO`点放置两个等量正电荷,在00`直线上有A、B、C三个点，且OA=0`B=0`C,一点电荷q(q>0) 沿路径Ⅰ从B运动到C电场力所做的功为W1, 沿路径Ⅱ从B运动到C电场力所做的功为W2, 同一点电荷在从A沿直线运动到C电场力所做的功为W3，则下列说法正确的是

A．W1大于W2         B．W1为负值
C．W1大于W3         D．W1等于W3

2012年9月25日，中国航母“辽宁舰”正式交付海军，这将极大提高我们中国海军的整体作战实力。如图所示是“歼—15飞机”在航母“辽宁舰”上的起降示意图。已知“歼—15飞机”的质量为m，它的发动机额定功率恒定，起飞前在航母上运动过程中所受的摩擦阻力为恒力。“歼—15飞机”以额定功率从静止开始沿航母做直线运动，到航母一端后起飞。设“歼—15飞机”经过时间t运动了位移s时，速度达到最大值v，此时刚好离开航母起飞。则“歼—15飞机”发动机在航母上运动过程所做的功为

A．B．
C．D．

如图所示，质量为m的物体放在光滑的水平面上，两次用力拉物体，都是从静止开始，以相同的加速度移动同样的距离，第一次拉力F1的方向水平，第二次拉力F2的方向与水平方向成α角斜向上，在此过程中，两力的平均功率为P1和P2，则(　　)

A．P1＜P2 B．P1＝P2 C．P1＞P2 D．无法判断

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网