题目内容
在火箭发射卫星的开始阶段,火箭与卫星竖直上升的运动可视为匀加速直线运动,加速度大小为a=5m/s2,封闭舱内,弹簧测力计上挂着一个质量m=9kg的物体,在卫星上升到某高度时,弹簧测力计示数为85N,求此时卫星与地面间的距离(地球半径为6400km,g=10m/s2)
分析:根据牛顿第二定律求出卫星在某一高度时的重力加速度大小,结合万有引力等于重力求出卫星与地面的距离.
解答:解:对封闭舱内的物体:T-mg'=ma,
所以g′=
=
m/s2=
m/s2
利用万有引力定律:
?
=(
)2,
代入数据解得:H=3200km.
答:卫星与地面间的距离为3200km.
所以g′=
| T-ma |
| m |
| 85-9×5 |
| 9 |
| 40 |
| 9 |
利用万有引力定律:
|
| g′ |
| g |
| R |
| R+H |
代入数据解得:H=3200km.
答:卫星与地面间的距离为3200km.
点评:本题考查了牛顿第二定律和万有引力定律的综合运用,掌握万有引力等于重力这一理论,并能灵活运用.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
 ,封闭舱内,弹簧测力计上挂着一个质量
,封闭舱内,弹簧测力计上挂着一个质量 的物体,在卫星上升到某高度时,弹簧测力计示数为85N,求此时卫星与地面间的距离(地球半径为
的物体,在卫星上升到某高度时,弹簧测力计示数为85N,求此时卫星与地面间的距离(地球半径为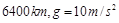 )
) ,封闭舱内,弹簧测力计上挂着一个质量
,封闭舱内,弹簧测力计上挂着一个质量 的物体,在卫星上升到某高度时,弹簧测力计示数为85N,求此时卫星与地面间的距离(地球半径为
的物体,在卫星上升到某高度时,弹簧测力计示数为85N,求此时卫星与地面间的距离(地球半径为 )
)