题目内容
20.从离地面500米的空中自由落下一个小球,取g=10m/s2求小球:(1)经过多长时间落到地面?
(2)自开始下落计时,在第1s内位移,最后1s内的位移,下落时间为总时间的一半时的位移.
(3)下落前半段位移与后半段位移所用时间比.
分析 根据高度,结合位移时间公式求出自由落体运动的时间.根据位移时间公式求出第1s内的位移和最后1s内的位移,以及下落时间为总时间一半时的位移.
根据位移时间公式求出下落前半位移和后半位移所用的时间之比.
解答 解:(1)根据h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×500}{10}}s=10s$.
(2)在第1s内的位移${x}_{1}=\frac{1}{2}g{{t}_{1}}^{2}=\frac{1}{2}×10×1m=5m$.
最后1s内的位移$x′=h-\frac{1}{2}gt{′}^{2}=500-\frac{1}{2}×10×81m=95m$.
下落时间为总时间一半时的位移${x}_{2}=\frac{1}{2}g{{t}_{2}}^{2}=\frac{1}{2}×10×25m=125m$.
(3)根据h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}$,
可知下落前半位移与整个位移所用的时间之比为1:$\sqrt{2}$,则下落前半位移与后半位移所用时间之比为1:$(\sqrt{2}-1)$.
答:(1)经过10s时间落到地面.
(2)第1s内的位移为5m,最后1s内的位移为95m,下落时间为总时间一半时的位移为125m.
(3)下落前半位移与后半位移所用时间之比为1:$(\sqrt{2}-1)$.
点评 解决本题的关键知道自由落体运动的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
相关题目
6. 如图所示为双缝干涉实验中产生的条纹图样,甲图为绿光进行实验的图样,a为中央亮条纹,乙为换用另一种单色光进行实验的图样,a′为中央亮条纹,则以下说法中正确的是( )
如图所示为双缝干涉实验中产生的条纹图样,甲图为绿光进行实验的图样,a为中央亮条纹,乙为换用另一种单色光进行实验的图样,a′为中央亮条纹,则以下说法中正确的是( )
 如图所示为双缝干涉实验中产生的条纹图样,甲图为绿光进行实验的图样,a为中央亮条纹,乙为换用另一种单色光进行实验的图样,a′为中央亮条纹,则以下说法中正确的是( )
如图所示为双缝干涉实验中产生的条纹图样,甲图为绿光进行实验的图样,a为中央亮条纹,乙为换用另一种单色光进行实验的图样,a′为中央亮条纹,则以下说法中正确的是( )| A. | 乙图可能是用红光实验产生的条纹,表明红光波长较长 | |
| B. | 乙图可能是用紫光实验产生的条纹,表明紫光波长较长 | |
| C. | 乙图可能是用紫光实验产生的条纹,表明紫光波长较短 | |
| D. | 乙图可能是用红光实验产生的条纹,表明红光波长较短 |
8.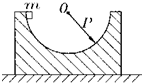 如图所示,半圆形的光滑固定轨道槽竖直放置,质量为m的小物体由顶端从静止开始下滑,则物体经过槽底时,对槽底的压力大小为( )
如图所示,半圆形的光滑固定轨道槽竖直放置,质量为m的小物体由顶端从静止开始下滑,则物体经过槽底时,对槽底的压力大小为( )
 如图所示,半圆形的光滑固定轨道槽竖直放置,质量为m的小物体由顶端从静止开始下滑,则物体经过槽底时,对槽底的压力大小为( )
如图所示,半圆形的光滑固定轨道槽竖直放置,质量为m的小物体由顶端从静止开始下滑,则物体经过槽底时,对槽底的压力大小为( )| A. | 2mg | B. | 3mg | C. | mg | D. | 5mg |
5.如图所示,长为L的细杆AB,从静止开始竖直落下,求它全部通过距下端h处P点所用时间是( )


| A. | $\sqrt{\frac{2h}{g}}$ | B. | $\sqrt{\frac{2(L+h)}{g}}-\sqrt{\frac{2h}{g}}$ | C. | $\sqrt{\frac{2(L+h)}{g}}$ | D. | $\sqrt{\frac{2(L+h)}{g}}-\sqrt{\frac{2L}{g}}$ |
9.关于磁通量,下列哪个说法是正确的( )
| A. | 穿过某一面积的磁感线条数叫做穿过这个面积的磁通量 | |
| B. | 穿过单位面积的磁感线条数与该面积的比值,叫做穿过这个面积的磁通量 | |
| C. | 某一面积与该处磁感强度的乘积,叫做穿过这个面积的磁通量 | |
| D. | 垂直穿过某一面积的磁感线条数与该面积的比值,叫做穿过这个面积的磁通量 |
 如图所示,OO′上侧有磁感应强度大小B=2.0×10-4T的匀强磁场,电子以V=1.6×106m/s的速度从A点与OO′垂直的方向进入磁场,在垂直于磁场的平面内运动.已知电子质量m=9.1×10-31kg、电量q=1.6×10-19C.
如图所示,OO′上侧有磁感应强度大小B=2.0×10-4T的匀强磁场,电子以V=1.6×106m/s的速度从A点与OO′垂直的方向进入磁场,在垂直于磁场的平面内运动.已知电子质量m=9.1×10-31kg、电量q=1.6×10-19C.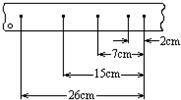 如图所示的纸带是由斜面下滑的小车通过打点计时器拉出来的,打点的时间间隔是0.02s,现按每10个点划分纸带,数据已标在图上,打点计时器打下第二个点是小车的速度为0.175m/s,小车运动的加速度为0.75m/s2.
如图所示的纸带是由斜面下滑的小车通过打点计时器拉出来的,打点的时间间隔是0.02s,现按每10个点划分纸带,数据已标在图上,打点计时器打下第二个点是小车的速度为0.175m/s,小车运动的加速度为0.75m/s2.