题目内容
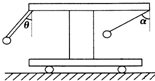 如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )分析:先对右侧球受力分析,运用牛顿第二定律求加速度,再对左侧球受力分析,根据牛顿第二定律求弹力的大小和方向.
解答:解:A、B、C、对右侧小球受力分析,受到重力和细线的拉力,根据牛顿第二定律,有
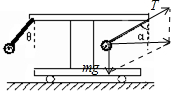
F合=mgtanα=ma
解得
a=gtanα
再对左侧小球受力分析,受到重力Mg和杆的弹力T,小球向右以加速度a做变速运动,设弹力与竖直方向的夹角为β,根据牛顿第二定律,有
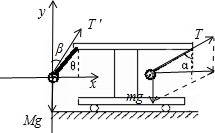
x方向:Tx=T′sinβ=Ma ①
y方向:Ty-Mg=Tcosβ-Mg=0 ②
根据牛顿第二定律,有
F′合=Ma=Mgtanθ ③
解得
θ=β
故A正确、B错误、C错误;
D、由于弹力不沿着杆的方向,故此时轻杆的形变包括拉伸形变与弯曲形变,故D正确;
故选AD.

F合=mgtanα=ma
解得
a=gtanα
再对左侧小球受力分析,受到重力Mg和杆的弹力T,小球向右以加速度a做变速运动,设弹力与竖直方向的夹角为β,根据牛顿第二定律,有

x方向:Tx=T′sinβ=Ma ①
y方向:Ty-Mg=Tcosβ-Mg=0 ②
根据牛顿第二定律,有
F′合=Ma=Mgtanθ ③
解得
θ=β
故A正确、B错误、C错误;
D、由于弹力不沿着杆的方向,故此时轻杆的形变包括拉伸形变与弯曲形变,故D正确;
故选AD.
点评:本题关键是先对右侧小球受力分析,得出加速度,再对左侧小球受力分析,根据牛顿第二定律求出杆的弹力的方向;要注意,杆的弹力可以沿着杆,也可以不沿着杆.

练习册系列答案
相关题目
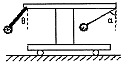 如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成a角,若θ<a,则下列说法正确的是( )
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成a角,若θ<a,则下列说法正确的是( )| A、轻杆对小球的弹力方向沿着轻杆方向向上 | B、轻杆对小球的弹力方向与细线平行 | C、轻杆对小球的弹力方向既不与细线平行,也不沿着轻杆方向 | D、此时小车的加速度为gtanα |
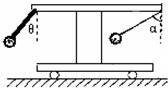 如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊另一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊另一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )| A、轻杆对小球的弹力方向一定沿着细绳方向向上 | B、轻杆对小球的弹力方向可能沿着轻杆方向向上 | C、此时小车的加速度可能为gtanθ | D、此时小车的加速度一定为gtanα |
 如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( ) 如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车做匀变速运动时,细线保持与竖直方向成α角,若θ<α,则下列哪一项说法正确的是( )
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车做匀变速运动时,细线保持与竖直方向成α角,若θ<α,则下列哪一项说法正确的是( )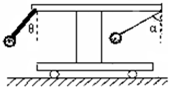 如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )