题目内容
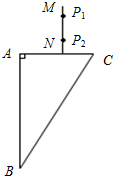
如图所示为一直角三棱镜截面,∠A=30°,∠C=90°,BC边长为L.一足够大的光屏MN平行于BC竖直放置.以MN为y轴建立如图所示直角坐标系,B点坐标为(-L,0).在0<y<L的范围内,一簇平行于AC的平行光射到AB面上.过AB中点的光线经AB面折射后恰好射向C点.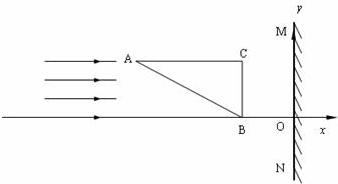
Ⅰ.求该棱镜的折射率.
Ⅱ.求光屏上有光照射到的坐标范围.

Ⅰ.求该棱镜的折射率.
Ⅱ.求光屏上有光照射到的坐标范围.
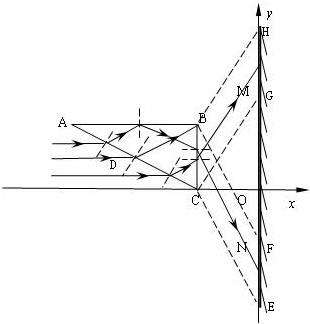
I、如右图所示:射向AB中点的光线的入射角为i=60°.
又因为D为AC的中点,△BCD为正三角形,折射角为r=30°.
所以折射率n=
=
=
(2)从DC段入射的光线经介质折射后平行于DB,以30°的入射角射向BC,折射角为60°,
则OG=Ltan60°=
L.则得 BC=HG.
所以,这部分光线的坐标范围为:
L~(1+
)L.
从AD段入射的光线经介质折射后平行于BD,以60°的入射角射向AB.由于sin60°>
,所以在AB面上发生全反射后再以30°的入射角射向BC,折射角为60°,
OE=Ltan60°=
L.则得 BC=EF.所以,这部分光线的坐标范围为:(1-
)L~-
L.
综上得,最后光屏上被照亮的坐标范围为:(1-
)L~-
L和
L~(1+
)L.
答:
Ⅰ.该棱镜的折射率是
.
Ⅱ.光屏上有光照射到的坐标范围是:(1-
)L~-
L和
L~(1+
)L.
又因为D为AC的中点,△BCD为正三角形,折射角为r=30°.
所以折射率n=
| sini |
| sinr |
| sin60° |
| sin30° |
| 3 |
(2)从DC段入射的光线经介质折射后平行于DB,以30°的入射角射向BC,折射角为60°,
则OG=Ltan60°=
| 3 |
所以,这部分光线的坐标范围为:
| 3 |
| 3 |
从AD段入射的光线经介质折射后平行于BD,以60°的入射角射向AB.由于sin60°>
| 1 |
| n |
OE=Ltan60°=
| 3 |
| 3 |
| 3 |
综上得,最后光屏上被照亮的坐标范围为:(1-
| 3 |
| 3 |
| 3 |
| 3 |
答:
Ⅰ.该棱镜的折射率是
| 3 |
Ⅱ.光屏上有光照射到的坐标范围是:(1-
| 3 |
| 3 |
| 3 |
| 3 |


练习册系列答案
相关题目