题目内容
13.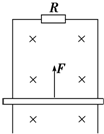 如图所示,竖直放置的两根平行金属导轨间距为l,之间接有定值电阻R,质量为m的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒的电阻为r,导轨电阻不计.整个装置放在磁感应强度为B的匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下先加速上升的一段时间,再达到稳定状态.则下列说法中正确的是( )
如图所示,竖直放置的两根平行金属导轨间距为l,之间接有定值电阻R,质量为m的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒的电阻为r,导轨电阻不计.整个装置放在磁感应强度为B的匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下先加速上升的一段时间,再达到稳定状态.则下列说法中正确的是( )| A. | 棒达到稳定状态时,通过它的电流为I=$\frac{(F-mg)}{Bl}$ | |
| B. | 棒达到稳定状态时,其速度为v=$\frac{(F-mg)R}{{B}^{2}{l}^{2}}$ | |
| C. | 棒达到稳定状态前,其加速度一直在减小 | |
| D. | 整个过程中,棒所受安培力做功在数值上等于棒上所生的热 |
分析 稳定前通过受力分析确定加速度的变化,当棒达到稳定状态时,即导体棒匀速运动合外力为零,对导体棒受力分析可求的电流大小和速度大小,根据能量守恒定律求解产生的热量.
解答 解:对导体棒受力分析得:F-mg-BIL=ma,而感应电动势E=BLV,电流I=$\frac{E}{R+r}$,带入得:$F-mg-\frac{{B}^{2}{L}^{2}V}{R+r}=ma$,随着运动速度V增加,加速度减小,当加速度减小到零时,速度最大v=$\frac{(F-mg)(R+r)}{{B}^{2}{L}^{2}}$,电流I=$\frac{F-mg}{BL}$,故A正确;B错误;C正确;
根据能量守恒定律可知,棒所受安培力做功在数值上等于回路中产生的焦耳热,故D错误;
故选:AC
点评 本题为电磁感应定律条件下,牛顿第二定律和能量守恒定律的应用题目,关键确定合外力变化中速度与加速度的过程分析题目.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
3.水的摩尔质量为18g/mol,密度为1g/cm3,则每个水分子的质量为2.99×10-26kg,每个水分子所占体积为2.99×10-29m3.(${N}_{A}=6.02×1{0}^{23}$个)
1.对于质量一定的物体,下列说法中正确的是( )
| A. | 物体的动能不变,则其速度一定也不变 | |
| B. | 物体的速度不变,则其动能一定也不变 | |
| C. | 物体的动能不变,说明物体的运动状态没有改变 | |
| D. | 物体的动能不变,说明物体所受的合外力一定为零 |
18.关于机械波,下列说法中正确的是( )
| A. | 机械波既能在介质中传播,也能在真空中传播 | |
| B. | 离波源较近的质点总比离波源较远的质点振动得早一些 | |
| C. | 机械波的传播速度与振源的振动速度相等 | |
| D. | 在一个周期内,沿着波的传播方向,振子随波移动一个波长的距离 |
5.对于温度,下列说法错误的是( )
| A. | 温度在宏观上反映物体的冷热程度 | |
| B. | 温度高的物体内所有分子的分子动能都大于温度低的物体内的所有分子 | |
| C. | 温度高的物体内有的分子的分子动能可以小于温度低的物体内的部分分子 | |
| D. | 温度高的物体的分子平均动能一定大于温度低的物体,与物质种类无关 |
3.某种气体的温度是0℃,可以说( )
| A. | 气体中分子的温度是0℃ | |
| B. | 气体中分子运动的速度快的温度一定高于0℃,运动慢的温度一定低于0℃,所以气体平均温度是0℃ | |
| C. | 气体温度升高时,速率小的分子数目减少,速率大的分子数目增加 | |
| D. | 该气体没有内能 |
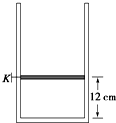 如图所示,足够长的圆柱形气缸竖直放置,其横截面积为1×10-3m2,气缸内有质量m=1kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底12cm,此时气缸内被封闭气体的压强1.5×105Pa,温度为300K.外界大气压为1.0×105Pa,g=10m/s2.
如图所示,足够长的圆柱形气缸竖直放置,其横截面积为1×10-3m2,气缸内有质量m=1kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底12cm,此时气缸内被封闭气体的压强1.5×105Pa,温度为300K.外界大气压为1.0×105Pa,g=10m/s2. 用F=10N的拉力在水平地面上拉物体由静止开始向右运动s=2m,如图所示.已知拉力和水平方向夹角是37°,物体与地面间的滑动摩擦因数μ=0.5,质量m=2kg,g取10 m/s2,sin37°=0.60,cos37°=0.80.求:
用F=10N的拉力在水平地面上拉物体由静止开始向右运动s=2m,如图所示.已知拉力和水平方向夹角是37°,物体与地面间的滑动摩擦因数μ=0.5,质量m=2kg,g取10 m/s2,sin37°=0.60,cos37°=0.80.求: