题目内容
12．对于做平抛运动的物体，下列说法中正确的是（ ）| A． | 飞行时间由初速度和高度共同决定 | |
| B． | 水平射程由初速度和高度共同决定 | |
| C． | 速度和加速度都时刻在变化 | |
| D． | 平抛运动速度变化量的方向沿曲线（运动轨迹）的切线方向 |
分析 平抛运动是具有水平方向的初速度只在重力作用下的运动，是一个匀变速曲线运动．解决平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究，水平方向做匀速直线运动，竖直方向做自由落体运动．运动时间由高度决定．
解答 解：A、平抛运动竖直方向做自由落体运动，根据h=$\frac{1}{2}g{t}^{2}$可知：t=$\sqrt{\frac{2h}{g}}$，运动时间由高度决定，与初速度无关，所以A错误；
B、根据x=v0t可知，水平位移由时间和初速度共同决定，时间又是由高度决定的，所以水平位移由初速度和高度决定，所以B正确；
C、做平抛运动的物体只受重力的作用，所以其加速度为重力加速度，加速度的大小时不变的，但是物体的速度在变化，所以C错误；
D、根据△v=gt可知，加速度不变，平抛运动速度变化量的方向沿竖直方向，所以D错误．
故选：B
点评 本题就是对平抛运动规律的考查，掌握住平抛运动的规律，水平方向上匀速直线运动，竖直方向上自由落体运动，根据匀速直线运动和自由落体运动的规律逐个分析即可．
练习册系列答案
53随堂测系列答案
相关题目
2．某同学欲采用如图所示的电路完成相关实验．图中电流表A的量程为0.6A，内阻约0.1Ω；电压表V的量程为3V，内阻约6kΩ；G为小量程电流表；电源电动势约3V，内阻较小．下列实验电路中正确的是（ ）
| A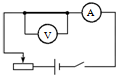． |  测定一段电阻丝（约5Ω）的电阻 | |
| B． |  测定电池的电动势和内阻（约2.0Ω） | |
| C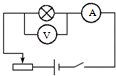． |  描绘小灯泡（额定电压2.5V）的伏安特性曲线 | |
| D． |  多用电表欧姆档测二极管正向电阻 |
如图所示，导线所围区域内有一垂直纸面向里的变化的匀强磁场，磁感强度按下列哪一图线所表示的方式随时间变化时，导体圆环将受到向上的磁场作用力（ ）
20．某同学利用透明直尺和光电计时器来验证机械能守恒定律，实验的简易示意图如图1所示，当有不透光物体从光电门间通过时，光电计时器就可以显示物体的挡光时间．所用的XDS-007光电门传感器可测的最短时间为0.01ms．将挡光效果好、宽度为d=3.8×10-3m的多段黑色磁带贴在透明直尺上，将直尺从一定高度由静止释放，并使其竖直通过光电门．某同学测得各段黑色磁带通过光电门的时间△ti与图中所示的高度差△hi-1，并将部分数据进行了处理，结果如表所示．查得当地重力加速度值为g=9.8m/s2，表中M为直尺质量．
（1）请将表格中的数据填写完整，计算结果均保留3位有效数字：v4=4.00m/s，△Ek3=$\frac{1}{2}$Mv42-$\frac{1}{2}$Mv12=3.07M，Mg△h3=3.14M
（2）根据该实验请你判断图2中△Ek-△h图象中正确的是C．
| i | △ti/10-3s | vi=$\frac{d}{△t}$/m•s-1 | △Eki-1=$\frac{1}{2}$Mvi2-$\frac{1}{2}$Mv12 | △hi-1/m | Mg△hi-1 |
| 1 | 1.21 | 3.14 | |||
| 2 | 1.15 | 3.30 | 0.52M | 0.0600 | 0.59M |
| 3 | 1.00 | 3.80 | 2.29M | 0.2400 | 2.35M |
| 4 | 0.95 | 0.3200 | |||
| 5 | 0.90 | 4.22 | 3.97M | 0.4100 | 4.02M |
（2）根据该实验请你判断图2中△Ek-△h图象中正确的是C．
7．如图所示，A球振动后，通过水平细绳迫使B、C振动．下列说法正确的是（ ）
| A． | 只有A、C两球的振动周期相等 | B． | C球的振幅比B球的振幅小 | ||
| C． | C球的振幅比B球的振幅大 | D． | A、B、C三球的振动周期相等 |
4．如图所示电路中，L1、L2、L3、L4是四只相同的电灯，当滑动变阻器
的滑片P向上滑动时，下列说法正确的是（ ）
的滑片P向上滑动时，下列说法正确的是（ ）| A． | L1变亮，L2变亮 | B． | L1变亮，L2变暗 | C． | L1变暗，L4变暗 | D． | L1变暗，L4变亮 |
1．下列说法符合物理学史实的是（ ）
| A． |  第谷发现了海王星和冥王星 | |
| B． |  开普勒发现了万有引力定律 | |
| C． |  牛顿发现了行星的运动规律 | |
| D． |  卡文迪许第一次在实验室里测出了万有引力常量 |
2．
如图所示，竖直平面内由两个半径分别为r1和r2的圆形过山车轨道N、P．若过山车在两个轨道的最高点对轨道的压力都恰好为零，则过山车在N、P最高点的速度比$\frac{{v}_{1}}{{v}_{2}}$为（ ）
如图所示，竖直平面内由两个半径分别为r1和r2的圆形过山车轨道N、P．若过山车在两个轨道的最高点对轨道的压力都恰好为零，则过山车在N、P最高点的速度比$\frac{{v}_{1}}{{v}_{2}}$为（ ）| A． | $\frac{{r}_{1}}{{r}_{2}}$ | B． | $\sqrt{\frac{{r}_{1}}{{r}_{2}}}$ | C． | $\frac{{r}_{2}}{{r}_{1}}$ | D． | $\sqrt{\frac{{r}_{2}}{{r}_{1}}}$ |