Question

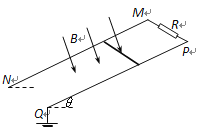
【题目】如图，空间存在两个水平方向等大反向的匀强磁场，水平虚线为其边界，磁场范围足够大。矩形多匝闭合线框ABCD下边位于两磁场边界处，匝数n=200，每匝质量为0．1kg，每匝电阻R=1Ω，边长AB=0．5m，BC=1．125m。一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮，一端连接线框，另一端连接质量为10kg的竖直悬挂绝缘物体P，且P受到F=70-200v（N）的竖直外力作用（v为线框的瞬时速度大小）。现将线框静止释放，刚运动时，外力F的方向竖直向下，线框中的电流随时间均匀增加。一段时间后撤去外力F，线框恰好开始做匀速直线运动。若细线始终绷紧，线框平面在运动过程中始终与磁场垂直，且CD边始终保持水平，重力加速度g=10m/s2，不计空气阻力。

（1）求空间中匀强磁场的磁感应强度B的大小？

（2）从开始运动到线框全部进入下方磁场过程所用时间t和绳上拉力的最大功率分别为多少？

（3）从开始运动到撤去外力过程中，线框产生的焦耳热为253J，则该过程流过单匝导线横截面的电量Q和外力F做功分别为多少？

Answer 1

【答案】（1） （2） ，50W （3） ，

【解析】(1)开始时电流随时间均匀增加，又因为

所以v随t均匀增加，线框做匀加速运动。则

联立解得：B=1T，a=1m/s2

(2) 匀速运动时

所以v0=0．5m/s则

匀加速过程中，研究物块P

T=180-200V

匀速运动过程中，研究物块P∶T=Mg，P′=Tv0=50W>40．5W

所以绳子拉力的最大功率为50W；

(3)因为

则

由动能定理：

解得：。