题目内容
如图是“研究匀变速直线运动”实验中获得的一条纸带，O、A、B、C、D和E为纸带上六个计数点．
（1）OD间的距离为
（2）如图是根据实验数据绘出的s-t2图线（s为各计数点至同一起点的距离），则由此图可算出加速度为
（1）OD间的距离为
1.20cm
1.20cm
；（2）如图是根据实验数据绘出的s-t2图线（s为各计数点至同一起点的距离），则由此图可算出加速度为
0.933
0.933
m/s2（保留三位有效数字）．分析：精度是1毫米刻度尺读数要估读到毫米的下一位，整数刻度用零补充位置，
根据解析式讨论图象斜率的意义．
根据解析式讨论图象斜率的意义．
解答：解：（1）最小刻度是毫米的刻度尺读数要估读到最小刻度的下一位，故拿零来补充估测值位置
所以OD间的距离为1.20cm．
（2）由匀变速直线运动公式x=
at2得知图象的斜率表示
a，即加速度的二分之一
计算斜率得：a=2k=0.933m/s2
故答案为：（1）1.20cm；（2）0.933
所以OD间的距离为1.20cm．
（2）由匀变速直线运动公式x=
| 1 |
| 2 |
| 1 |
| 2 |
计算斜率得：a=2k=0.933m/s2
故答案为：（1）1.20cm；（2）0.933
点评：本题考查了打点计时器实验中图象处理数据的方法，原理是匀变速直线运动的规律，是一道基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
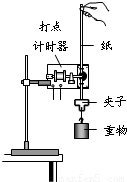
（1）如图所示为用打点计时器验证机械能守恒定律的实验装置．关于这一实验，下列说法中正确的是
（1）如图所示为用打点计时器验证机械能守恒定律的实验装置。关于这一实验，下列说法中正确的是( )
