题目内容
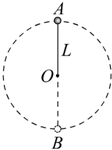
 如图所示,用轻绳系住质量为m的小球,使小球在竖直平面内绕点O做圆周运动.小球做圆周运动的半径为L.小球在最高点A的速度大小为v.求:
如图所示,用轻绳系住质量为m的小球,使小球在竖直平面内绕点O做圆周运动.小球做圆周运动的半径为L.小球在最高点A的速度大小为v.求:
(1)小球在最高点A时,绳子上的拉力大小;
(2)小球在最低点B时,绳子上的拉力大小.
 解:(1)小球在A点受力如图1所示.重力与绳子拉力F1的合力提供小球向心力,根据牛顿第二定律有
解:(1)小球在A点受力如图1所示.重力与绳子拉力F1的合力提供小球向心力,根据牛顿第二定律有 mg+F1=

所以,拉力F1=
 -mg
-mg(2)小球从A点到B点运动过程,根据机械能守恒,有
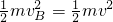 +2mgL,
+2mgL,所以,vB=
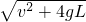
小球在B点受力如图2所示,重力与绳子拉力F2的合力提供小球向心力,则有
F2-mg=
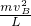
所以,F2=
 +5mg.
+5mg.答:
(1)小球在最高点A时,绳子上的拉力大小是
 -mg;
-mg;(2)小球在最低点B时,绳子上的拉力大小是
 +5mg.
+5mg.分析:(1)小球在最高点时,由重力和轻绳的拉力的合力提供小球的向心力,根据牛顿第二定律求解绳子的拉力大小.
(2)小球从A点到B点运动过程遵从机械能守恒,由机械能守恒定律求出小球经过最低点时的速度,再牛顿第二定律求解小球在最低点B时,绳子上的拉力大小.
点评:圆周运动往往与其他知识综合在一起,本题是圆周运动与机械能守恒定律的综合.常见问题,不难.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
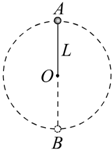 如图所示,用轻绳系住质量为m的小球,使小球在竖直平面内绕点O做圆周运动.小球做圆周运动的半径为L.小球在最高点A的速度大小为v.求:
如图所示,用轻绳系住质量为m的小球,使小球在竖直平面内绕点O做圆周运动.小球做圆周运动的半径为L.小球在最高点A的速度大小为v.求: