题目内容
13.如图所示,某同学在做“研究匀变速直线运动”实验中,用使用f=50HZ交流电的打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点之间还有四个试验点未画出,其中s1,s2,s3,s4,s5,s6表示相邻计数点间的距离.则D点处瞬时速度的大小表达式是$\frac{f({{s}_{3}+s}_{4})}{10}$,小车运动的加速度计算表达式为$\frac{{f}^{2}{(s}_{4}+{{s}_{5}+s}_{6}-{{s}_{1}-s}_{2}{-s}_{3})}{225}$.小车加速度大小a大小为0.20m/s2(保留两位有效数字)
分析 根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上D点时小车的瞬时速度大小.
解答 解:由于每相邻两个计数点间还有4个点没有画出,所以相邻的计数点间的时间间隔T=$\frac{5}{f}$=0.1s,
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上D点时小车的瞬时速度大小.
vD=$\frac{f({{s}_{3}+s}_{4})}{10}$,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:s4-s1=3a1T2
s5-s2=3a2T2
s6-s3=3a3T2
为了更加准确的求解加速度,我们对三个加速度取平均值
得:a=$\frac{1}{3}$(a1+a2+a3)
小车运动的加速度计算表达式为a=$\frac{{f}^{2}{(s}_{4}+{{s}_{5}+s}_{6}-{{s}_{1}-s}_{2}{-s}_{3})}{225}$
代入数据得a=0.20m/s2.
故答案为:$\frac{f({{s}_{3}+s}_{4})}{10}$;$\frac{{f}^{2}{(s}_{4}+{{s}_{5}+s}_{6}-{{s}_{1}-s}_{2}{-s}_{3})}{225}$;0.20
点评 要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.在研究物体的运动时,下列物体中可以当作质点处理的是( )
| A. | 作直线运动的物体可以看作质点 | |
| B. | 体操运动员在做单臂大回环,可以视为质点 | |
| C. | 确定轮船在大海中的位置时,可以把它当作质点来处理 | |
| D. | 研究火车通过路旁一根电线杆的时间时,火车可以当作质点来处理 |
4.在宽度为d的河中,水流速度为v2,船在静水中速度为v1(且v1<v2),航向可以选.现让该船开始渡河,则该船( )
| A. | 可能的最短渡河时间为$\frac{d}{v_2}$ | |
| B. | 可能的最短渡河位移为d | |
| C. | 若船头垂直河岸渡河,河水流速越大,渡河时间越长 | |
| D. | 不管船头与河岸夹角是多少,此船都不可能垂直河岸渡河到达正对岸 |
18. 如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率V2(V2>V1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率V2(V2>V1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
 如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率V2(V2>V1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率V2(V2>V1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )| A. | 滑块返回传送带右端时的速率为V2 | |
| B. | 此过程中传送带对滑块做功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 | |
| C. | 此过程中滑块与传送带间摩擦产生的热量为 m(v1+v2)2 | |
| D. | 此过程中电动机做功为mv1(v1+v2) |
2.水平桌面上一重200N的物体,物体与桌面间的最大静摩擦力为45N,物体与桌面间的滑动摩擦系数为0.2,现分别用15N,30N,80N的水平拉力拉此物体时,物体受到的摩擦力依次为( )
| A. | 15N,30N,40N | B. | 0N,15N,15N | C. | 0N,20N,40N | D. | 15N,40N,40N |
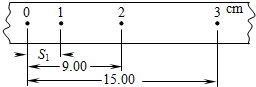 在做“测定匀变速直线运动的加速度”的实验中,取下一段纸带研究其运动情况,如图所示.设0点为计数的起始点,两计数点之间的时间间隔为0.1秒,则0点到1点之间的距离S1为4.00cm,打1计数点时物体的瞬时速度为0.45m/s,物体的加速度为1.0m/s2.
在做“测定匀变速直线运动的加速度”的实验中,取下一段纸带研究其运动情况,如图所示.设0点为计数的起始点,两计数点之间的时间间隔为0.1秒,则0点到1点之间的距离S1为4.00cm,打1计数点时物体的瞬时速度为0.45m/s,物体的加速度为1.0m/s2.