题目内容
(2010?顺义区二模)如图所示,一小滑块(可视为质点)质量为m=3.0kg,它在距平台边缘s=4.0m以v0=5.0m/s的速度向右运动,滑块与平台面间的动摩擦因数μ=0.2,滑块运动到平台边缘后从平台水平抛出,恰能沿圆弧切线从A点进入光滑竖直圆弧轨道,A、B为圆弧两端点,其连线水平.已知圆弧半径为R=1.0m,对应圆心角为θ=106°,平台与AB连线的高度差为h.(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)求:
(1)滑块运动到平台边缘时的速度v;(2)滑块从平台抛出到A点的时间t;
(3)滑块运动到圆弧轨道最低点O时对轨道的压力N.

(1)滑块运动到平台边缘时的速度v;(2)滑块从平台抛出到A点的时间t;
(3)滑块运动到圆弧轨道最低点O时对轨道的压力N.

分析:(1)对物体从开始运动到平台边缘的过程中运用动能定理即可求解;
(2)根据恰能沿圆弧切线从A点进入光滑竖直圆弧轨道求出A点的竖直方向速度,再根据平抛运动的规律求解;
(3)根据牛顿第二定律及机械能守恒定律即可求解.
(2)根据恰能沿圆弧切线从A点进入光滑竖直圆弧轨道求出A点的竖直方向速度,再根据平抛运动的规律求解;
(3)根据牛顿第二定律及机械能守恒定律即可求解.
解答:解:(1)对物体从开始运动到平台边缘的过程中运用动能定理得:
mv2-
mv02=μmgs
解得:v=3m/s
(2)运动员离开平台后至A的过程中做平抛运动,则
在A点有:vy=vtan
=4m/s
在竖直方向做自由落体运动,t=
=0.4s
(3)运动员在圆弧轨道做圆周运动,
由牛顿第二定律可得 N-mg=m
由机械能守恒得
mv2+mg[h+R(1-cos53°)]=
mvo2
解得N=129N
根据牛顿第三定律得:滑块运动到圆弧轨道最低点O时对轨道的压力为129N.
答:(1)滑块运动到平台边缘时的速度为3m/s;(2)滑块从平台抛出到A点的时间为0.4s;(3)滑块运动到圆弧轨道最低点O时对轨道的压力为129N
| 1 |
| 2 |
| 1 |
| 2 |
解得:v=3m/s
(2)运动员离开平台后至A的过程中做平抛运动,则
在A点有:vy=vtan
| θ |
| 2 |
在竖直方向做自由落体运动,t=
| vy |
| g |
(3)运动员在圆弧轨道做圆周运动,
由牛顿第二定律可得 N-mg=m
| vo2 |
| R |
由机械能守恒得
| 1 |
| 2 |
| 1 |
| 2 |
解得N=129N
根据牛顿第三定律得:滑块运动到圆弧轨道最低点O时对轨道的压力为129N.
答:(1)滑块运动到平台边缘时的速度为3m/s;(2)滑块从平台抛出到A点的时间为0.4s;(3)滑块运动到圆弧轨道最低点O时对轨道的压力为129N
点评:本题是一个综合性较强的题目,在题目中滑块先做匀减速运动,再做平抛运动,最后在圆轨道内做的是圆周运动,难度适中.

练习册系列答案
相关题目
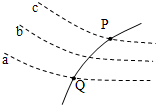 (2010?顺义区二模)如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,Uab=Ubc,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
(2010?顺义区二模)如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,Uab=Ubc,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( ) (2010?顺义区二模)压敏电阻的阻值随所受压力的增大而减小.某实验小组在升降机水平地面上利用压敏电阻设计了判断升降机运动状态的装置.其工作原理图如图甲所示,将压敏电阻、定值电阻R、电流显示器、电源E连成电路,在压敏电阻上放置一个绝缘重物.0~t1时间内升降机停在某一楼层处,t1时刻升降机开始运动,从电流显示器中得到电路中电流i随时间t变化情况如图乙所示.则下列判断正确的是( )
(2010?顺义区二模)压敏电阻的阻值随所受压力的增大而减小.某实验小组在升降机水平地面上利用压敏电阻设计了判断升降机运动状态的装置.其工作原理图如图甲所示,将压敏电阻、定值电阻R、电流显示器、电源E连成电路,在压敏电阻上放置一个绝缘重物.0~t1时间内升降机停在某一楼层处,t1时刻升降机开始运动,从电流显示器中得到电路中电流i随时间t变化情况如图乙所示.则下列判断正确的是( )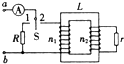 (2010?顺义区二模)如图所示,L为理想变压器,其原线圈、副线圈的匝数分别为n1、n2.
(2010?顺义区二模)如图所示,L为理想变压器,其原线圈、副线圈的匝数分别为n1、n2. 为理想交流电流表,阻值分别为R、r的两个定值电阻接在电路中.将a、b两端接到电压恒定的交流电源上,当开关S分别拨至接线柱l和2时,发现电流表的示数相同.则两个定值电阻的阻值之比r/R等于( )
为理想交流电流表,阻值分别为R、r的两个定值电阻接在电路中.将a、b两端接到电压恒定的交流电源上,当开关S分别拨至接线柱l和2时,发现电流表的示数相同.则两个定值电阻的阻值之比r/R等于( )