Question

(1)开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即＝k，k是一个对所有行星都相同的常量．将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量k的表达式．已知引力常数为G，太阳的质量为M_太．

(2)开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统(如地月系统)都成立．经测定月地距离为3.84×10⁸ m，月球绕地球运动的周期为2.36×10⁶ s，试计算地球的质量M_地．(G＝6. 67×10^－11 N·m²/kg²，结果保留一位有效数字)

 

Answer 1

【答案】

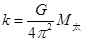 6×10²⁴kg

【解析】

试题分析：（1）因行星绕太阳作匀速圆周运动，于是轨道的半长轴a即为轨道半径r．根据万有引力定律和牛顿第二定律有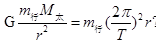              ①

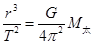于是有             ②

即 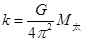                  ③                        （6分）

(2)G＝m_月r，M_地＝

代入数值解得：M_地＝6×10²⁴kg                           （6分）

考点：本题就是考察学生对开普勒行星运动第三定律的理解和应用，

点评：掌握住开普勒行星运动第三定律和万有引力定律即可求得结果，式中的常量k必修是相对于同一个中心天体来说的．