题目内容
(2011?南通模拟)(1)下列说法中正确的是
A.全息照片用激光来拍摄,主要是利用了激光的相干性
B.在光的双缝干涉实验中,将入射光由红光改为紫光,则条纹间距变宽
C.如果测量到来自遥远星系上的元素发出的光波长变长,这说明星系正在远离我们而去
D.拍摄玻璃橱窗内的物品时,在镜头前加一个偏振片可以增加透射光的强度
(2)如图(1)为频率f=1Hz的波源产生的横波,图中虚线左侧为A介质,右侧为B介质.其中x=14m处的质点振动方向向上.则该波在A、B两种介质中传播的速度之比vA:vB=
(3)如图(2)所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1.对紫光的折射率为n2.在距AC边d处有一与AC平行的光屏.现有由以上两种色光组成的很细的光束垂直AB边射入棱镜.
①红光和紫光在棱镜中的传播速度比为多少?
②若两种光都能从AC面射出,求在光屏MN上两光点间的距离.
AC
AC
A.全息照片用激光来拍摄,主要是利用了激光的相干性
B.在光的双缝干涉实验中,将入射光由红光改为紫光,则条纹间距变宽
C.如果测量到来自遥远星系上的元素发出的光波长变长,这说明星系正在远离我们而去
D.拍摄玻璃橱窗内的物品时,在镜头前加一个偏振片可以增加透射光的强度

(2)如图(1)为频率f=1Hz的波源产生的横波,图中虚线左侧为A介质,右侧为B介质.其中x=14m处的质点振动方向向上.则该波在A、B两种介质中传播的速度之比vA:vB=
2:3
2:3
.若图示时刻为0时刻,则经0.75s处于x=6m的质点位移为5
5
cm(3)如图(2)所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1.对紫光的折射率为n2.在距AC边d处有一与AC平行的光屏.现有由以上两种色光组成的很细的光束垂直AB边射入棱镜.
①红光和紫光在棱镜中的传播速度比为多少?
②若两种光都能从AC面射出,求在光屏MN上两光点间的距离.
分析:(1)全息照片利用激光的单色性,即相干性来拍摄的.光的双缝条纹间距与波长成正比,红光的波长比紫光长,条纹间距大.来自遥远星系上的元素发出的光波长变长,频率变小,产生多普勒效应,说明星系离我们的距离越来越大.由于玻璃的折射,常常照片模糊不清,而经过玻璃反射的光是偏振光,在镜头前加一个偏振片可以减弱折射光,而使图象清晰.
(2)波在A、B两种介质中传播的频率相同,由图读出波长之比,再求波速之比.x=14m处的质点振动方向向上,波向左传播,则此时x=6m的质点正向下振动,经0.75s时该质点到达波峰.
(3)由公式v=
,求解红光和紫光在棱镜中的传播速度比.根据折射定律求出两种光在AC面上的折射角,由几何知识在光屏MN上两光点间的距离.
(2)波在A、B两种介质中传播的频率相同,由图读出波长之比,再求波速之比.x=14m处的质点振动方向向上,波向左传播,则此时x=6m的质点正向下振动,经0.75s时该质点到达波峰.
(3)由公式v=
| c |
| n |
解答:解:
(1)A、全息照片利用激光的单色性,即相干性来拍摄的.故A正确.
B、在光的双缝干涉实验中,将入射光由红光改为紫光,则条纹间距变窄.故B错误.
C、来自遥远星系上的元素发出的光波长变长,频率变小,产生多普勒效应,说明星系离我们的距离越来越大.故C正确.
D、由于玻璃的折射,常常照片模糊不清,而经过玻璃反射的光是偏振光,在镜头前加一个偏振片可以减弱折射光,而使图象清晰,并没有增强透射光的强度.故D错误.
故选AC
(2)波在A、B两种介质中传播的频率f相同.由图读出波长分别是:λA=4m,λB=6m.由公式v=λf得到,该波在A、B两种介质中传播的速度之比vA:vB=2:3.
该波的周期T=
=1s.经0.75s时处于x=6m的质点到达波峰,位移y=5cm.
(3)①由v红=
,v紫=
得
=
②设红光和紫光在AC面上的折射角分别为r1、r2.根据折射定律得
=n1
=n2
由几何知识得
x=d(tanr2-tanr1)=d(
-
)
故答案为:
(1)AC;(2)2:3;5;(3)①红光和紫光在棱镜中的传播速度比为
=
;在光屏MN上两光点间的距离是d(
-
).
(1)A、全息照片利用激光的单色性,即相干性来拍摄的.故A正确.
B、在光的双缝干涉实验中,将入射光由红光改为紫光,则条纹间距变窄.故B错误.
C、来自遥远星系上的元素发出的光波长变长,频率变小,产生多普勒效应,说明星系离我们的距离越来越大.故C正确.
D、由于玻璃的折射,常常照片模糊不清,而经过玻璃反射的光是偏振光,在镜头前加一个偏振片可以减弱折射光,而使图象清晰,并没有增强透射光的强度.故D错误.
故选AC
(2)波在A、B两种介质中传播的频率f相同.由图读出波长分别是:λA=4m,λB=6m.由公式v=λf得到,该波在A、B两种介质中传播的速度之比vA:vB=2:3.
该波的周期T=
| 1 |
| f |
(3)①由v红=
| c |
| n1 |
| c |
| n2 |
| v红 |
| v紫 |
| n2 |
| n1 |
②设红光和紫光在AC面上的折射角分别为r1、r2.根据折射定律得
| sinr1 |
| sin30° |
| sinr2 |
| sin30° |
由几何知识得
x=d(tanr2-tanr1)=d(
| n2 | ||||
|
| n1 | ||||
|
故答案为:
(1)AC;(2)2:3;5;(3)①红光和紫光在棱镜中的传播速度比为
| v红 |
| v紫 |
| n2 |
| n1 |
| n2 | ||||
|
| n1 | ||||
|
点评:本题考查的内容比较多,有物理光学、几何光学和机械波等知识点较多,但难度不大.

练习册系列答案
相关题目
 (2011?南通模拟)如图所示,一块长度为a、宽度为b、厚度为d的金属导体,当加有与侧面垂直的匀强磁场B,且通以图示方向的电流I时,用电压表测得导体上、下表面MN间电压为U.已知自由电子的电量为e.下列说法中正确的是( )
(2011?南通模拟)如图所示,一块长度为a、宽度为b、厚度为d的金属导体,当加有与侧面垂直的匀强磁场B,且通以图示方向的电流I时,用电压表测得导体上、下表面MN间电压为U.已知自由电子的电量为e.下列说法中正确的是( ) (2011?南通模拟)如图所示,A、B两小球用轻杆连接,竖直放置.由于微小的扰动,A球沿竖直光滑槽运动,B球沿水平光滑槽运动.则在A球到达底端前( )
(2011?南通模拟)如图所示,A、B两小球用轻杆连接,竖直放置.由于微小的扰动,A球沿竖直光滑槽运动,B球沿水平光滑槽运动.则在A球到达底端前( )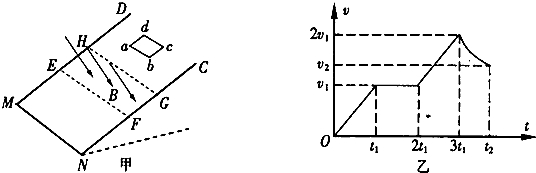
 (2011?南通模拟)如图所示,水平面上放置质量为M的三角形斜劈,斜劈顶端安装光滑的定滑轮,细绳跨过定滑轮分别连接质量为m1和m2的物块.m1在斜面上运动,三角形斜劈保持静止状态.下列说法中正确的是( )
(2011?南通模拟)如图所示,水平面上放置质量为M的三角形斜劈,斜劈顶端安装光滑的定滑轮,细绳跨过定滑轮分别连接质量为m1和m2的物块.m1在斜面上运动,三角形斜劈保持静止状态.下列说法中正确的是( )