题目内容
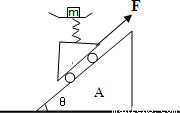
 如图,倾角为θ质量为2m的斜面体放在水平面上,质量为m的物块位于斜面上,不计一切摩擦,给斜面体加一水平向左的推力.求:
如图,倾角为θ质量为2m的斜面体放在水平面上,质量为m的物块位于斜面上,不计一切摩擦,给斜面体加一水平向左的推力.求:(1)当斜面体静止,物块在斜面体上自由下滑时,需要加的水平推力F的大小;
(2)当物块和斜面体相对静止一起沿水平面运动时,需要加的水平推力F的大小.
(3)求(1)、(2)两种情况下物块对斜面体的压力之比.
分析:(1)先隔离物快求出二者之间的弹力,再以斜面体为研究对象,利用平衡态列方程求解.(2)二者恰好不发生相对滑动时,二者的加速度相同,以A为研究对象,根据牛顿第二定律可求出A加速度.以整体为研究对象,根据牛顿第二定律求解推力.(3)分别求出两种情况物体与斜面体弹力,利用牛顿第三定律求比值.
解答:解:(1)当斜面体静止,物块在斜面体上自由下滑时,以物快为研究对象,受重力和斜面体的弹力N1.
则有:N1=mgcosθ
再以斜面体为研究对象,受重力、推力、地面对斜面体向上的弹力和物快对斜面体写详细的弹力(据牛顿第三定律知N1与N'1作用力和反作用力),如图所示.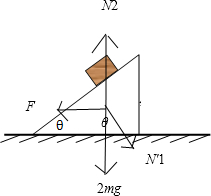
由于斜面体静止,故斜面体所受的合外力为零,
所以F=N'sinθ=mgsinθcosθ;
(2)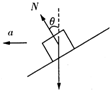 物块和斜面体相对静止一起沿水平面运动时,二者具有共同的加速度.取整体为研究对象,水平方向应用牛顿第二定律,有F=(2m+m)a
物块和斜面体相对静止一起沿水平面运动时,二者具有共同的加速度.取整体为研究对象,水平方向应用牛顿第二定律,有F=(2m+m)a
隔离出物快,其受力示意图如图,N=
根据牛顿第二定律,则有mgtanθ=ma
解得a=gtanθ
联立求解F=(2m+m)a=3mgtanθ
(3)由以上可知两种情况下物块与斜面体的弹力分别为mgcosθ和
,
据牛顿第三定律得:两种情况下物块对斜面体的压力分别为mgcosθ和
,
所以两种情况下物块对斜面体的压力之比为cos2θ
答:(1)当斜面体静止,物块在斜面体上自由下滑时,需要加的水平推力F的大小mgsinθcosθ;
(2)当物块和斜面体相对静止一起沿水平面运动时,水平推力F的大小3mgtanθ
(3)求(1)、(2)两种情况下物块对斜面体的压力之比cos2θ
则有:N1=mgcosθ
再以斜面体为研究对象,受重力、推力、地面对斜面体向上的弹力和物快对斜面体写详细的弹力(据牛顿第三定律知N1与N'1作用力和反作用力),如图所示.

由于斜面体静止,故斜面体所受的合外力为零,
所以F=N'sinθ=mgsinθcosθ;
(2)
 物块和斜面体相对静止一起沿水平面运动时,二者具有共同的加速度.取整体为研究对象,水平方向应用牛顿第二定律,有F=(2m+m)a
物块和斜面体相对静止一起沿水平面运动时,二者具有共同的加速度.取整体为研究对象,水平方向应用牛顿第二定律,有F=(2m+m)a 隔离出物快,其受力示意图如图,N=
| mg |
| cosθ |
根据牛顿第二定律,则有mgtanθ=ma
解得a=gtanθ
联立求解F=(2m+m)a=3mgtanθ
(3)由以上可知两种情况下物块与斜面体的弹力分别为mgcosθ和
| mg |
| cosθ |
据牛顿第三定律得:两种情况下物块对斜面体的压力分别为mgcosθ和
| mg |
| cosθ |
所以两种情况下物块对斜面体的压力之比为cos2θ
答:(1)当斜面体静止,物块在斜面体上自由下滑时,需要加的水平推力F的大小mgsinθcosθ;
(2)当物块和斜面体相对静止一起沿水平面运动时,水平推力F的大小3mgtanθ
(3)求(1)、(2)两种情况下物块对斜面体的压力之比cos2θ
点评:本题的关键根据运动状态,灵活选取研究对象,即采用隔离法和整体法相结合,用牛顿第二定律求解.

练习册系列答案
相关题目
 如图所示,质量为m的木块放到倾角为θ的斜面上,恰好可以沿斜面匀速下滑,问:
如图所示,质量为m的木块放到倾角为θ的斜面上,恰好可以沿斜面匀速下滑,问: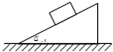 如图,倾角为α质量为M的斜面与水平面间、斜面与质量为m的木块间的动摩擦因数均为μ,木块由静止开始沿斜面加速下滑时斜面仍保持静止.求水平面给斜面的摩擦力大小和方向以及斜面对水平面的压力.
如图,倾角为α质量为M的斜面与水平面间、斜面与质量为m的木块间的动摩擦因数均为μ,木块由静止开始沿斜面加速下滑时斜面仍保持静止.求水平面给斜面的摩擦力大小和方向以及斜面对水平面的压力.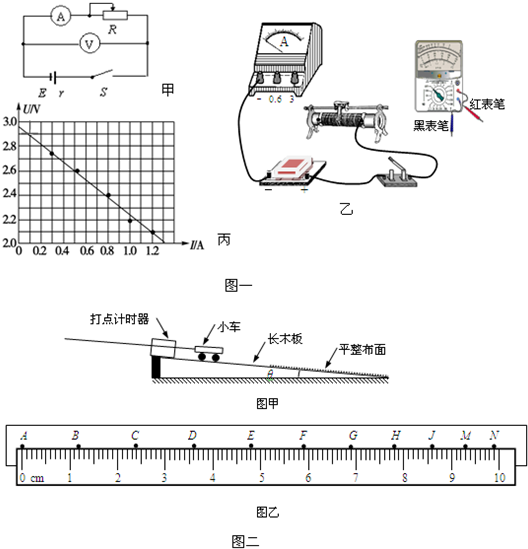
 拟如图所示,质量为80kg的物体放在安装在小车上的水平磅秤上,小车在平行于斜面的拉力F作用下沿斜面无摩擦地向上运动,现观察到物体在磅秤上读数为1000N.已知斜面倾角θ=30°,小车与磅秤的总质量为20kg.
拟如图所示,质量为80kg的物体放在安装在小车上的水平磅秤上,小车在平行于斜面的拉力F作用下沿斜面无摩擦地向上运动,现观察到物体在磅秤上读数为1000N.已知斜面倾角θ=30°,小车与磅秤的总质量为20kg. ,斜面质量为100kg,试求斜面对地面的压力和摩擦力分别为多少?(A一直静止在地面上)
,斜面质量为100kg,试求斜面对地面的压力和摩擦力分别为多少?(A一直静止在地面上)