题目内容
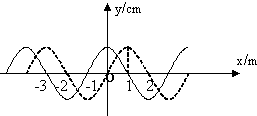
一列简谐波在某一时刻的波形如图中实线所示，若经过一段时间后，波形变成图中虚线所示，波的速度大小为1m/s，那么这段时间可能是（ ）
| A、1s | B、2s | C、3s | D、4s |
分析：由图读出波长，由波速公式求出周期，根据波形平移和波的周期性，确定时间t的可能值．
解答：解：由图读出波长为λ=4m，由波速公式v=
得到，周期T=
=
s=4s
若波向左传播时，时间t的通项为t=（n+
）T=（4n+3）s，n=0，1，2，…
即t=3s、7s、11s、…
若波向右传播时，时间t的通项为t=（k+
）T=（4k+1）s，k=0，1，2，…
即t=1s、5s、9s、…
故时间t可以是：1s、3s、5s、7s、9s、…
故选：AC．
| λ |
| T |
| λ |
| v |
| 4 |
| 1 |
若波向左传播时，时间t的通项为t=（n+
| 3 |
| 4 |
即t=3s、7s、11s、…
若波向右传播时，时间t的通项为t=（k+
| 1 |
| 4 |
即t=1s、5s、9s、…
故时间t可以是：1s、3s、5s、7s、9s、…
故选：AC．
点评：本题知道两个时刻的波形，要考虑波传播方向的双向性，及时间的周期性，根据通项得到特殊值．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
如图是一列简谐波在某一时刻的波形图线．虚线是0.2s后它的波形图线．这列波可能的传播速度是多大？
如图所示是一列简谐波在某一时刻的波形，则（ ）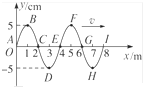
图所示的是一列简谐波在某一时刻的波形图象，下列说法中正确的是（ ）
