题目内容
一根细绳与一个轻弹簧,上端分别固定在A、B两点,下端C点共同拉住一个小钢球,如图所示,AC、BC与竖直方向的夹角均为θ,则( )

A.烧断细绳的瞬间,小球的加速度a=
| ||
| B.烧断细绳的瞬间,小球的加速度a=gsinθ | ||
C.弹簧在C处与小球断开的瞬间,小球的加速度a=
| ||
| D.弹簧在C处与小球断开的瞬间,小球的加速度a=gsinθ |

A、B、对球受力分析,受重力、弹簧的拉力F和细线的拉力T,如图所示:
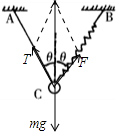
根据平衡条件,有:
F=T=
;
断开细线瞬间,弹簧弹力和重力不变,故合力变为
,沿着细线的反方向;
故加速度为
,沿着细线的反方向,故A正确,B错误;
C、D、弹簧在C处与小球断开的瞬间,小球受重力和细线的拉力,变为单摆,合力等于重力的切向分力,根据牛顿第二定律,有:mgsinθ=ma,解得a=gsinθ;故C错误,D正确;
故选AD.

根据平衡条件,有:
F=T=
| mg |
| 2cosθ |
断开细线瞬间,弹簧弹力和重力不变,故合力变为
| mg |
| 2cosθ |
故加速度为
| g |
| 2cosθ |
C、D、弹簧在C处与小球断开的瞬间,小球受重力和细线的拉力,变为单摆,合力等于重力的切向分力,根据牛顿第二定律,有:mgsinθ=ma,解得a=gsinθ;故C错误,D正确;
故选AD.

练习册系列答案
相关题目
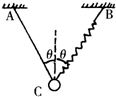 一根细绳与一个轻弹簧,上端分别固定在A、B两点,下端C点共同拉住一个小钢球,如图所示,AC、BC与竖直方向的夹角均为θ,则( )
一根细绳与一个轻弹簧,上端分别固定在A、B两点,下端C点共同拉住一个小钢球,如图所示,AC、BC与竖直方向的夹角均为θ,则( )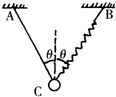



 一根细绳与一个轻弹簧,上端分别固定在A、B两点,下端在C点共同拉住一个小钢球,如图所示,AC、BC与竖直方向的夹角均为
一根细绳与一个轻弹簧,上端分别固定在A、B两点,下端在C点共同拉住一个小钢球,如图所示,AC、BC与竖直方向的夹角均为