题目内容
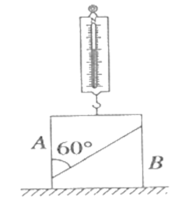
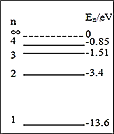
【题目】如图所示,一个内壁光滑的圆锥筒固定在竖直面内。有两个质量不同的小球甲和乙贴着筒的内壁在水平面内做匀速圆周运动。则
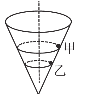
A. 甲乙两球都是由重力和支持力的合力提供向心力
B. 筒壁对甲球的支持力等于筒壁对乙球的支持力
C. 甲球的运动周期大于乙球的运动周期
D. 甲球的角速度大于乙球的角速度
【答案】AC
【解析】
对两球受力分析即可得向心力的来源；支持力与重力的合力提供小球所需要的向心力，根据平衡条件即可得支持力大小关系；利用牛顿第二定律列式，结合两球的轨道半径关系即可分析出两球的周期与角速度关系．
A、对两球受力分析，都受重力、支持力两个力的作用，由于做匀速圆周运动，即合外力提供向心力，故可知甲、乙两球都是由重力与支持力的合力提供向心力，A正确；
BCD、设圆锥筒的顶角为
，则有：在竖直方向有：
，轨道平面内有：
，联立可得支持力为：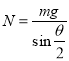
，角速度为：
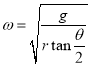，由于两球的质量不同，则可知两球所受支持力大小不相等，由图可知甲球的轨道半径大于乙球的轨道半径，故甲球的角速度小于乙的角速度，根据
可知，甲球的周期大于乙球的周期，BD错误C正确．
练习册系列答案
相关题目
