题目内容
3.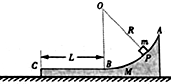 如图所示,一工件置于水平地面上,其AB段为一半径R=1m的光滑圆弧轨道,BC段为一长度L=$\frac{7}{6}$m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,其中P点为圆弧轨道上的一个确定点,离BC轨道的高度h=0.2m,一个可视为质点的物块,其质量m=0.1kg,与BC间的摩擦因数μ=0.3,已知工件质量M=0.6kg,工件与地面的动摩擦因数μ=0.3,取g=10m/s2.
如图所示,一工件置于水平地面上,其AB段为一半径R=1m的光滑圆弧轨道,BC段为一长度L=$\frac{7}{6}$m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,其中P点为圆弧轨道上的一个确定点,离BC轨道的高度h=0.2m,一个可视为质点的物块,其质量m=0.1kg,与BC间的摩擦因数μ=0.3,已知工件质量M=0.6kg,工件与地面的动摩擦因数μ=0.3,取g=10m/s2.(1)将物块由C点以4m/s的初速度滑上轨道,求物块滑至点B时对轨道的压力的大小;
(2)若使物块保持在P点并于工件一起向左做匀加速直线运动,则作用于工件上的水平恒力F的大小;
(3)当物块保持在P点并与工件一起向左加速至6m/s时,若使工件立刻停止运动(即不考虑减速的时间),物块飞离圆弧轨道落至BC段,则物块的落点距B点多远?
分析 (1)由动能定理可以求出B点速度;对B点由向心力公式可求得B处工件受到的压力;再由牛顿第三定律可求得压力;
(2)对物体、工件和物体整体分析,根据牛顿第二定律求解;
(3)根据平抛运动的规律和几何关系求解.
解答 解:(1)①物块从C点下滑经B点过程,
由动能定理得:-μmgL=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$,
对B点分析知FN-mg=m$\frac{{v}_{B}^{2}}{R}$
代入数据解得:FN=3.3N;
由牛顿第三定律可求得压力为3.3N
(2)设物块的加速度大小为a,P点与圆心的连线与竖直方向间的夹角为θ,由几何关系可得:
cosθ=$\frac{R-h}{R}$
对物体,由牛顿第二定律得:mgtanθ=ma,
对工件和物体整体,由牛顿第二定律得:
F-μ(M+m)g=(M+m)a,
代入数据解得:F=2.65N;
(3)物体做平抛运动,
在竖直方向上:h=$\frac{1}{2}$gt2,
水平方向:x1=vt,
x2=x1-Rsinθ,
联立并代入数据解得:x2=0.6m;
答:(1)将物块由C点以4m/s的初速度滑上轨道,物块滑至点B时对轨道的压力的大小为3.3N;
(2)若使物块保持在P点并于工件一起向左做匀加速直线运动,则作用于工件上的水平恒力F的大小为2.65N;
(3)当物块保持在P点并与工件一起向左加速至6m/s时,若使工件立刻停止运动(即不考虑减速的时间),物块飞离圆弧轨道落至BC段,则物块的落点距B点距离为0.6m.
点评 本题考查了求高度差、求力与距离问题,物体运动过程较复杂,分析清楚物体运动过程是正确解题的前提与关键,应用动能定理、牛顿第二定律、平抛运动的规律等即可正确解题,解题时要注意受力分析.

 直线P1P2过均匀玻璃球球心O,细光束a、b平行且关于P1P2对称,由空气射入玻璃球的光路如图.a、b光相比( )
直线P1P2过均匀玻璃球球心O,细光束a、b平行且关于P1P2对称,由空气射入玻璃球的光路如图.a、b光相比( )| A. | 玻璃对a光的折射率较小 | B. | 玻璃对a光的临界角较小 | ||
| C. | b光在玻璃中的传播速度较大 | D. | b光在玻璃中的传播时间较短 |
| A. | 位移和路程都是描述物体位置变化的物理量 | |
| B. | 速度的变化率和速率都是矢量 | |
| C. | 跳水比赛时,为了研究运动员的技术动作,可将运动员视为质点 | |
| D. | “卧看满天云不动,不知云与我俱东”此两句诗的前半句是以诗人自己为参考系的 |
| A. | 固体、液体、气体中都有扩散运动和布朗运动 | |
| B. | 热量能够从高温物体传到低温物体,但不能从低温物体传到高温物体 | |
| C. | 利用阿伏伽德罗常数,气体的摩尔质量和密度,可以估算出气体分子间的平均距离 | |
| D. | 当分子间的距离r=r0时,斥力等于引力,表现出分子力为零 | |
| E. | 扩散运动和布朗运动的剧烈程度都与温度有关 |
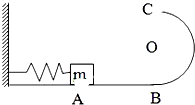 如图所示,光滑水平面AB与竖直面内的半圆形轨道在B点衔接,导轨半径为R,一个质量为m的静止物块在A处压缩弹簧,在弹力的作用下获某一向右速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,求:
如图所示,光滑水平面AB与竖直面内的半圆形轨道在B点衔接,导轨半径为R,一个质量为m的静止物块在A处压缩弹簧,在弹力的作用下获某一向右速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,求: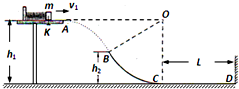 如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存的弹性势能Ep=2J.现打开锁扣K,物块与弹簧分离后将以一定的水平速度向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,小物块沿轨道BCD运动并与右边的竖直墙壁会发生碰撞,重力加速度g=10m/s2,空气阻力忽略不计.试求:
如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存的弹性势能Ep=2J.现打开锁扣K,物块与弹簧分离后将以一定的水平速度向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,小物块沿轨道BCD运动并与右边的竖直墙壁会发生碰撞,重力加速度g=10m/s2,空气阻力忽略不计.试求: 如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块Q相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及P与桌面之间的动摩擦因数都μ=0.4,物块P重为40N,物块Q重为20N,滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F拉P使它做匀速运动,则:
如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块Q相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及P与桌面之间的动摩擦因数都μ=0.4,物块P重为40N,物块Q重为20N,滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F拉P使它做匀速运动,则: