题目内容
 如图,两根光滑绝缘细棒在同一竖直平面内,两棒均与水平面成45°角.棒上各穿一个质量为10g、电荷量为10-7C的带正电的小球.求:
如图,两根光滑绝缘细棒在同一竖直平面内,两棒均与水平面成45°角.棒上各穿一个质量为10g、电荷量为10-7C的带正电的小球.求:(1)两球在同一高度相距10cm处滑下时的加速度多大?
(2)两球从上述位置同时下滑,当它们相距多远时,两球速度最大?
分析:(1)根据库仑定律,结合牛顿第二定律,及力的平行四边形定则,即可求解;
(2)根据加速度为零时,速度达到最大,结合库仑定律,即可求解.
(2)根据加速度为零时,速度达到最大,结合库仑定律,即可求解.
解答: 解:(1)当相距10cm,且处在同一高时,球受到库仑力为:F库=
解:(1)当相距10cm,且处在同一高时,球受到库仑力为:F库=
=
N=9×10-3N;
对一小球受力分析,如图所示,则其合力在棒的方向为:F合=ma=Gcos45°-F库cos45°;
代入数据,解得:a=
=
m/s2=6.43m/s2;
(2)经分析,当速度达到最大时,其在棒方向的加速度为零,
即Gcos45°-F库cos45°=0;
又库仑定律可知,F库=
=G;
代入数据,解得:r=
=
m=3×10-2 m.
答:(1)两球在同一高度相距10cm处滑下时的加速度6.43m/s2;
(2)两球从上述位置同时下滑,当它们相距3×10-2 m时,两球速度最大.
 解:(1)当相距10cm,且处在同一高时,球受到库仑力为:F库=
解:(1)当相距10cm,且处在同一高时,球受到库仑力为:F库=| kQq |
| r2 |
| 9×109×10-7×10-7 |
| 0.12 |
对一小球受力分析,如图所示,则其合力在棒的方向为:F合=ma=Gcos45°-F库cos45°;
代入数据,解得:a=
| Gcos45°-F库cos45° |
| m |
10×10-3×10×
| ||||||||
| 10×10-3 |
(2)经分析,当速度达到最大时,其在棒方向的加速度为零,
即Gcos45°-F库cos45°=0;
又库仑定律可知,F库=
| kQq |
| r2 |
代入数据,解得:r=
|
|
答:(1)两球在同一高度相距10cm处滑下时的加速度6.43m/s2;
(2)两球从上述位置同时下滑,当它们相距3×10-2 m时,两球速度最大.
点评:考查库仑定律与牛顿第二定律的应用,注意加速度为零时,速度达到最大,同时注意正确的运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
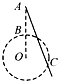 (2008?绵阳模拟)如图,在竖直圆的圆心口固定一负点电荷,A点在圆心口的正上方,B为圆周的最高点,C是圆周上的一点,一根光滑绝缘细杆固定在AC位置.有两个质量和电荷量都相同的带正电小球a、b,先让a穿在细杆上从A点静止开始沿杆滑下,后让b从A点静止开始下落,竖直运动.下述说法正确的是( )
(2008?绵阳模拟)如图,在竖直圆的圆心口固定一负点电荷,A点在圆心口的正上方,B为圆周的最高点,C是圆周上的一点,一根光滑绝缘细杆固定在AC位置.有两个质量和电荷量都相同的带正电小球a、b,先让a穿在细杆上从A点静止开始沿杆滑下,后让b从A点静止开始下落,竖直运动.下述说法正确的是( )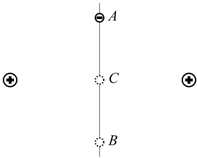 (2011?浙江模拟)如图所示,竖直放置一根光滑绝缘细直杆,在其两侧对称固定放置有两个等电荷量的正电荷.细杆上有A、B、C三点,其中C在两电荷的连线和细杆的交点位置,AC=CB=h.一个带负电、质量为m的小球串在细杆上,从A点静止释放运动到B点,则下列说法正确的是( )
(2011?浙江模拟)如图所示,竖直放置一根光滑绝缘细直杆,在其两侧对称固定放置有两个等电荷量的正电荷.细杆上有A、B、C三点,其中C在两电荷的连线和细杆的交点位置,AC=CB=h.一个带负电、质量为m的小球串在细杆上,从A点静止释放运动到B点,则下列说法正确的是( )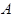 、
、 、
、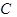 三点,其中
三点,其中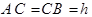 。一个带负电、质量为
。一个带负电、质量为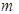 的小球串在细杆上,从
的小球串在细杆上,从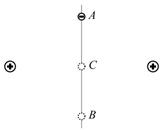

 、
、 、
、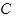 三点,其中
三点,其中 。一个带负电、质量为
。一个带负电、质量为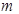 的小球串在细杆上,从
的小球串在细杆上,从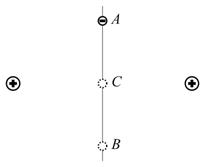
 之间往复运动
之间往复运动