题目内容
3.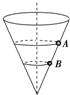 一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,如图所示,A的运动半径较大,则( )
一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,如图所示,A的运动半径较大,则( )| A. | A球的角速度必小于B球的角速度 | |
| B. | A球的线速度必小于B球的线速度 | |
| C. | A球的运动周期必大于B球的运动周期 | |
| D. | A球对筒壁的压力必大于B球对筒壁的压力 |
分析 对小球受力分析,受重力和支持力,合力提供向心力,根据牛顿第二定律列式求解即可.
解答 解:A、以小球为研究对象,对小球受力分析,小球受力如图所示,
由牛顿第二定律得:mgtanθ=m$\frac{{v}^{2}}{r}$,
解得:v=$\sqrt{grtanθ}$,
则ω=$\frac{v}{r}$=$\sqrt{\frac{gtanθ}{r}}$,
T=$\frac{2π}{ω}$=2π$\sqrt{\frac{r}{tanθ}}$,
由图示可知,对于AB两个球来说,重力加速度g与角θ相同,
A的转动半径大,B的半径小,因此,A的角速度小于B的角速度,A的线速度大于B的线速度,A的周期大于B的周期,故AC正确,B错误;
D、由受力分析图可知,球受到的支持力FN=$\frac{mg}{sinθ}$,由于两球的质量m与角度θ相同,则桶壁对AB两球的支持力相等,由牛顿第三定律可知,两球对桶壁的压力相等,故D错误;
故选:AC.
点评 本题关键是对小球受力分析,然后根据牛顿第二定律和向心力公式列式求解分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.关于某一物体的动能的下列说法正确的是( )
| A. | 如果物体的动能有变化,其速度也一定变化 | |
| B. | 如果物体的速度有变化,其动能也一定变化 | |
| C. | 如果合外力对物体做负功,其动能就一定减小 | |
| D. | 如果物体的动能没有变化,就一定没有外力对物体做功 |
18.甲、乙两车沿平直公路从某地同时同向驶向同一目的地,甲车在前一半时间内以速度v1作匀速运动,在后一半时间内以速度v2作匀速运动,乙车在前一半路程中以速度v1作匀速运动,后一半路程中以速度v2作匀速运动.下列判断正确的是( )
| A. | 如果v1大于v2,甲车先到达目的地 | B. | 如果v1大于v2,乙车先到达目的地 | ||
| C. | 如果v1小于v2,甲车先到达目的地 | D. | 如果v1小于v2,乙车先到达目的地 |
8.如图所示,OA、OB、OC三根细绳能承受的最大拉力完全一样,如果物体重力超过某一限度时,则绳子( )
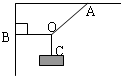

| A. | OA段先断 | B. | OB段先断 | C. | OC段先断 | D. | 一起断 |
13.下列说法正确的是( )
| A. | 电压与电动势的单位都是伏特,所以电压与电动势是同一物理量的不同叫法 | |
| B. | 导体中没有电流时,说明导体中的自由电荷没有移动 | |
| C. | 电动势越大,说明非静电力在电源内部把单位正电荷从负极移到正极做功越多 | |
| D. | 由公式E=$\frac{W}{q}$,电动势E的大小与非静电力做的功W成正比,与移送电荷量q成反比 |
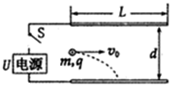 如图所示,水平放置的平行板电容器的极板长L=0.4m,两板间距离d=4×10-3m;在电容器两板不带电的情况下,有一束带电粒子,以相同的速率v0从两板中央沿平行极板方向水平射入两板之间,粒子流恰好落在下板的正中央;已知每个带电粒子的质量m=4×10-5kg,电量q=+1×10-8C.重力加速度g=10m/s2.为使粒子流能从平行板电容器的右侧射出电场,求:
如图所示,水平放置的平行板电容器的极板长L=0.4m,两板间距离d=4×10-3m;在电容器两板不带电的情况下,有一束带电粒子,以相同的速率v0从两板中央沿平行极板方向水平射入两板之间,粒子流恰好落在下板的正中央;已知每个带电粒子的质量m=4×10-5kg,电量q=+1×10-8C.重力加速度g=10m/s2.为使粒子流能从平行板电容器的右侧射出电场,求: