题目内容
2.有一横截面积为S的铜导线,流经其中的电流为I,设每单位体积的导线有n个自由电子,电子电量为e,此时电子的定向转动速度为v,在△t时间内,通过导体横截面的自由电子数目可表示为( )| A. | nvS△t | B. | nv△t | C. | $\frac{I}{(△te)}$ | D. | $\frac{I△t}{(Se)}$ |
分析 首先根据电流强度的定义可以求得t时间内通过导线横截面积的总的电荷量的大小,进而可以求得自由电子的个数,再根据电流的微观的表达式,根据电阻的运动的速率的大小也可以求得通过导线横截面的自由电子的个数.
解答 解:在t时间内,以速度v移动的电子在铜导线中通过的距离为vt,由于铜导线的横截面积为S,则在t时间内,电子经过的导线体积为:V=v△tS.
又由于单位体积的导线有n个自由电子,则在t时间内,通过导线横截面的自由电子数目可表示为:N=nvS△t.
由于流经导线的电流为I,则在t时间内,流经导线的电荷量为Q=It,而电子的电荷量为e,则t时间内通过导线横截面的自由电子数目可表示为:
N=$\frac{I△t}{e}$,故A正确.BCD错误
故选:A.
点评 本题计算自由电子的个数,要注意从不同的角度来分析问题,一是从微观运动的角度,二是从电流强度的角度全面分析求解.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
12.下列四组共点力分别作用于同一物体上,其中不可能使物体作匀速直线运动的是( )
| A. | 1N,4N,6N | B. | 2N,4N,6N | C. | 3N,4N,6N | D. | 4N,4N,6N |
10.关于向心力的说法中,正确的是( )
| A. | 物体由于做圆周运动而产生了向心力 | |
| B. | 做匀速圆周运动物体的向心力是恒力 | |
| C. | 做匀速圆周运动物体的向心力,一定等于其所受的合力 | |
| D. | 向心力只能改变物体的线速度方向,不能改变线速度的大小 |
7.下列说法中正确的是( )
| A. | 只有直接接触的物体之间才会有弹力的作用 | |
| B. | 力的大小可以用天平来直接测量 | |
| C. | 形状规则的物体,它的重心不一定在其几何中心 | |
| D. | 重力的方向一定垂直于接触面向下 |
15.一带电粒子从电场中的A点运动到B点,实线为电场线虚线为其运动轨迹,不计粒子所受重力,则( )
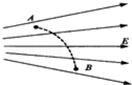

| A. | 粒子带正电 | B. | 粒子加速度逐渐减小 | ||
| C. | 粒子的电势能不断减小 | D. | 粒子的速度不断增加 |