题目内容
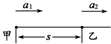 如图所示,处于平直轨道上的甲、乙两物体相距为s,同时、同向开始运动.甲以初速度v、加速度a1做匀加速直线运动,乙做初速度为零、加速度为a2的匀加速直线运动,假设甲能从乙旁边通过,要使甲、乙相遇两次的条件是( )
如图所示,处于平直轨道上的甲、乙两物体相距为s,同时、同向开始运动.甲以初速度v、加速度a1做匀加速直线运动,乙做初速度为零、加速度为a2的匀加速直线运动,假设甲能从乙旁边通过,要使甲、乙相遇两次的条件是( )分析:根据甲乙两车速度相等时,甲车的位移大于乙车的位移与s之和,求出s的范围,从而根据两车有二次相遇得出加速度的大小关系.
解答:解:若甲与乙速度相等时,甲已经从乙旁经过,则有:
v+a1t=a2t
vt+
a1t2>s+
a2t2
两式联立可得:s<
,
若再有a2>a1,则定有乙再次追上甲的结果,即甲、乙相遇两次.故B正确,A、C、D错误.
故选B.
v+a1t=a2t
vt+
| 1 |
| 2 |
| 1 |
| 2 |
两式联立可得:s<
| v2 |
| 2(a2-a1) |
若再有a2>a1,则定有乙再次追上甲的结果,即甲、乙相遇两次.故B正确,A、C、D错误.
故选B.
点评:本题属于运动学中的追及问题,掌握匀变速运动的运动学公式,并能灵活运用.

练习册系列答案
相关题目
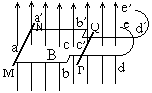 如图所示,abcde和a'b'c'd'e'为两平行的光滑导轨,其中abcd和a'b'c'd'部分为处于水平面内的直轨,ab、a'b'的间距为cd、c'd'间距的2倍;de和d'e'部分为与直轨相切的、半径均为R的半圆形轨道,处于竖直平面内.直轨部分处于竖直向上的匀强磁场中,弯轨部分处于匀强磁场外.在靠近aa'和cc'处放有两根金属棒MN、PQ,质量分别为2m和m.为使棒PQ能沿导轨运动并通过半圆形轨道的最高点ee',在初始位置必须至少给棒MN以多大的冲量?
如图所示,abcde和a'b'c'd'e'为两平行的光滑导轨,其中abcd和a'b'c'd'部分为处于水平面内的直轨,ab、a'b'的间距为cd、c'd'间距的2倍;de和d'e'部分为与直轨相切的、半径均为R的半圆形轨道,处于竖直平面内.直轨部分处于竖直向上的匀强磁场中,弯轨部分处于匀强磁场外.在靠近aa'和cc'处放有两根金属棒MN、PQ,质量分别为2m和m.为使棒PQ能沿导轨运动并通过半圆形轨道的最高点ee',在初始位置必须至少给棒MN以多大的冲量?