题目内容
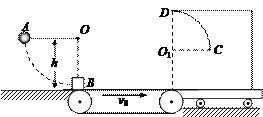
【题目】如下图所示，小球A系在细线的一端，线的另一端固定在O点，O点到光滑水平面的距离为h＝0.8m。已知A的质量为m，物块B的质量是小球A的5倍，静止于水平传送带左端的水平面上且位于O点正下方，传送带右端有一带半圆光滑轨道的小车，小车的质量是物块B的5倍，水平面、传送带及小车的上表面平滑连接，物块B与传送带的动摩擦因数μ＝0.5，其余摩擦不计，传送带长L＝3.5m，以恒定速率v0=6m/s顺时针运转。现拉动小球使线水平伸直后由静止释放，小球运动到最低点时与物块发生正碰，小球反弹后上升到最高点时与水平面的距离为
。若小车不固定，物块刚好能滑到与圆心O1等高的C点。重力加速度为g=10m/s2，小球与物块均可视为质点。求：
（1）小球与物块相碰后物块B的速度vB大小。
（2）若滑块B的质量mB=1kg，求滑块B与传送带之间因摩擦而产生的热量Q及带动传
送带的电动机多做的功W电。
（3）小车上的半圆轨道半径R大小。
【答案】(1) 
(2)Q=12.5J, 
(3)R=1.5m
【解析】（1）小球A下摆及反弹上升阶段机械能守恒，由机械能守恒定律得：
①
②
B碰撞过程系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得：
mvA=－mv1+5mvB③
代入数据解得： vB=1（m/s）④
（2）经过时间t，B与传送带速度相等，由匀变速直线运动速度公式得：
v0=vB+at ⑤
μmBg =vBa ⑥
代入数据解得：t=1（s） ⑥
物块滑行的距离： 
⑦
传送带的位移：S传=vt=6（m）⑧
则：Sx=S传-S物=2.5（m） ⑨
滑块B与传送带之间因摩擦而产生的热量：Q=μmBg Sx= 12.5(J)⑩
电动机多做的功
代入数据解得：W电＝30（J）
（3）物块在传送带上一直加速到达右端时恰好与传送带速度相等,系统水平方向动量守恒,以向右为正方向,由动量守恒定律得： 5mv0=(5m+25m)v
由机械能守恒定律得： 
代入数据解得：R＝1.5（m）
