题目内容
一只蚂蚁从蚂蚁洞沿直线爬出，已知爬出速度v的大小与距蚂蚁洞中心的距离L成反比，当蚂蚁到达距蚂蚁洞中心的距离L1=1m的A点时，速度大小为v1=20cm/s，问当蚂蚁到达距蚂蚁洞中心的距离L2=2m的B点时，其速度大小为v2="?" 蚂蚁从A点到达B点所用的时间t=?
v2="0.1m/s " Δt= 7.5s
由已知可得：蚂蚁在距离洞中心上处的速度v为v=k
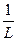，代入已知得：k=vL=0.2×1m2/s="0.2" m2/s，所以当L2=2m时，其速度v2=0.1m/s由速度的定义得：蚂蚁从L到L+ΔL所需时间Δt为
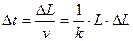……………………①类比初速度为零的匀加速直线运动的两个基本公式
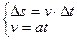
在t到t+Δt时刻所经位移Δs为
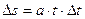………………②比较①、②两式可以看出两式的表述形式相同。
据此可得蚂蚁问题中的参量t和L分别类比为初速度为零的匀加速直线运动中的s和t，而
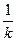相当于加速度a。于是，类比s=
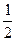a t2可得：在此蚂蚁问题中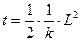
令t1对应L1，t2对应L2，则所求时间为
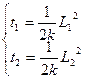
代入已知可得从A到B所用时间为：
Δt=t2－t1=
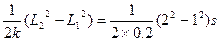="7.5s " 
练习册系列答案
相关题目
