题目内容
如图(甲)所示,一小型发电机内的矩形线圈在匀强磁场中以恒定的角速度ω绕垂直于磁场方向的固定轴转动,线圈匝数n=100匝.穿过每匝线圈的磁通量Φ随时间按正弦规律变化,如图(乙)所示,已知感应电动势的最大值Em=nωφm,其中φm为穿过每匝线圈磁通量的最大值,π=3.14,
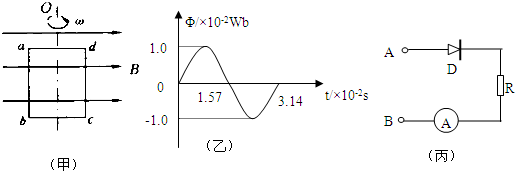
(1)求该发电机的感应电动势的最大值Em;
(2)请写出感应电动势e的瞬时表达式;
(3)将该发电机的输出端接到如图(丙)所示的电路A、B端,已知发电机线圈内阻为r=10Ω,图(丙)中的D为理想二极管(正向电阻为零,反向电阻无穷大),R=90Ω,求交流电流表的读数I.

(1)求该发电机的感应电动势的最大值Em;
(2)请写出感应电动势e的瞬时表达式;
(3)将该发电机的输出端接到如图(丙)所示的电路A、B端,已知发电机线圈内阻为r=10Ω,图(丙)中的D为理想二极管(正向电阻为零,反向电阻无穷大),R=90Ω,求交流电流表的读数I.
分析:(1)由乙图看出周期和最大磁通量,根据Em=nωφm求出最大值;
(2)根据e=Emcosωt 即可求出感应电动势e的瞬时表达式;
(3)根据电流的热效应即可求解.
(2)根据e=Emcosωt 即可求出感应电动势e的瞬时表达式;
(3)根据电流的热效应即可求解.
解答:解:(1)由图可知:T=3.14×10-2s,φm=1.0×10-2Wb
可求得:ω=
=200 rad/s
Em=nωφm=200 V
(2)e=Emcosωt=200cos 200t V
(3)根据闭合电路欧姆定律得:I=
=
=
A
根据电流热效应可得:I2R?
+0=I′2RT
代入数据得:I=
A
答:(1)求该发电机的感应电动势的最大值Em为200V;
(2)感应电动势e的瞬时表达式为200cos 200t V;
(3)交流电流表的读数为
A.
可求得:ω=
| 2π |
| T |
Em=nωφm=200 V
(2)e=Emcosωt=200cos 200t V
(3)根据闭合电路欧姆定律得:I=
| E |
| R+r |
| ||||
| R+r |
| 2 |
根据电流热效应可得:I2R?
| T |
| 2 |
代入数据得:I=
| 2 |
答:(1)求该发电机的感应电动势的最大值Em为200V;
(2)感应电动势e的瞬时表达式为200cos 200t V;
(3)交流电流表的读数为
| 2 |
点评:本题考查交变电流最大值、有效值的理解和应用的能力,对于交流电表的测量值、计算交流电功率、电功等都用到有效值.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目