题目内容
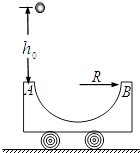
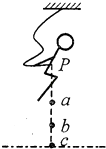
【题目】如图所示，一个小球从高h=10m处以水平速度v0=10m/s抛出，撞在倾角θ=45°的斜面上的P点，已知AC=5m，求：（g=10m/s2）
（1）P、C之间的距离；
（2）小球撞击P点时速度的大小．
【答案】
（1）
解：设P、C之间的距离为L，根据平抛运动规律，5+Lcos45°=v0t
h﹣Lsin45°= 
gt2，
联立解得：L=5 
m，t=1s
（2）
解：小球撞击P点时的水平速度v∥=v0=10m/s，
竖直速度vy=gt=10m/s．
小球撞击P点时速度的大小为v= 
=10 m/s，
设小球的速度方向与水平方向的夹角为α，则tanα= 
=1，α=45°，方向垂直于斜面向下．所以小球垂直于斜面向下撞击P点
【解析】小球做平抛运动，竖直方向做自由落体运动，根据位移时间公式即可求解；水平方向做匀速直线运动，根据位移时间公式结合几何关系即可求解．
【考点精析】利用平抛运动对题目进行判断即可得到答案，需要熟知特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动．
练习册系列答案
相关题目
