题目内容
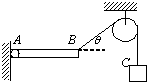 如图所示,均匀细杆AB质量为M,A端装有转轴,B端连接细线通过滑轮和质量为m的重物C相连,若杆AB呈水平,细线与水平方向夹角为θ 时恰能保持平衡,则杆对轴A有作用力大小下面表达式中正确的有( )
如图所示,均匀细杆AB质量为M,A端装有转轴,B端连接细线通过滑轮和质量为m的重物C相连,若杆AB呈水平,细线与水平方向夹角为θ 时恰能保持平衡,则杆对轴A有作用力大小下面表达式中正确的有( )分析:杆AB呈水平,处于静止状态,合力为零.对AB杆进行受力分析,因为AB杆处于平衡,受到重力、绳子拉力以及铰链对杆子的作用力处于平衡,根据三力汇交原理,求出轴对杆的作用力大小.由牛顿第三定律得到轴对杆的作用力大小.
解答: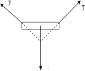 解:AB杆受重力Mg、绳子拉力T以及轴对杆子的作用力F处于平衡,合力为零,如图,根据三力汇交原理,拉力与水平方向的夹角为θ.根据平衡和对称性得知,F=T,在竖直方向上有:
解:AB杆受重力Mg、绳子拉力T以及轴对杆子的作用力F处于平衡,合力为零,如图,根据三力汇交原理,拉力与水平方向的夹角为θ.根据平衡和对称性得知,F=T,在竖直方向上有:
2Tsinθ=Mg.又T=mg,则F=
.
根据对称性可知,F=mg
根据平衡条件知:T与Mg的合力与F等大,反向,则由数学知识得:F=
=
故选ABC
 解:AB杆受重力Mg、绳子拉力T以及轴对杆子的作用力F处于平衡,合力为零,如图,根据三力汇交原理,拉力与水平方向的夹角为θ.根据平衡和对称性得知,F=T,在竖直方向上有:
解:AB杆受重力Mg、绳子拉力T以及轴对杆子的作用力F处于平衡,合力为零,如图,根据三力汇交原理,拉力与水平方向的夹角为θ.根据平衡和对称性得知,F=T,在竖直方向上有:2Tsinθ=Mg.又T=mg,则F=
| Mg |
| 2sinθ |
根据对称性可知,F=mg
根据平衡条件知:T与Mg的合力与F等大,反向,则由数学知识得:F=
| (Mg)2+T2+2Mg?Tcos(90°+θ) |
| M2g2-2Mmgsinθ+m2g2 |
故选ABC
点评:解决本题的关键能够正确地进行受力分析,根据三力汇交原理求出绳子拉力的大小.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
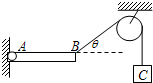 如图所示,均匀细杆AB的质量为M,A端装有固定转轴,B端连接细线通过滑轮和重物C相连,若杆AB呈水平,细线与水平方向的夹角为θ 时恰能保持平衡,则重物C的质量m=
如图所示,均匀细杆AB的质量为M,A端装有固定转轴,B端连接细线通过滑轮和重物C相连,若杆AB呈水平,细线与水平方向的夹角为θ 时恰能保持平衡,则重物C的质量m= 如图所示,均匀细杆AB的质量为mAB=5kg,A端装有固定转轴,B端连接细线通过滑轮和重物C相连,若杆AB呈水平,细线与水平方向的夹角为θ=30°时恰能保持平衡,则重物C的质量mC=
如图所示,均匀细杆AB的质量为mAB=5kg,A端装有固定转轴,B端连接细线通过滑轮和重物C相连,若杆AB呈水平,细线与水平方向的夹角为θ=30°时恰能保持平衡,则重物C的质量mC=