题目内容
【题目】如图所示,光滑水平面上有一质量M=1.98kg的小车,车的B点右侧的上表面是粗糙水平轨道,车的B点的左侧固定以半径R=0.7m的![]() 光滑圆弧轨道,圆弧轨道与水平轨道在B点相切,车的最右端D点固定轻质弹簧弹簧处于自然长度其左端正好对应小车的C点,B与C之间距离L=0.9m,一个质量m=2kg的小物块,置于车的B点,车与小物块均处于静止状态,突然有一质量
光滑圆弧轨道,圆弧轨道与水平轨道在B点相切,车的最右端D点固定轻质弹簧弹簧处于自然长度其左端正好对应小车的C点,B与C之间距离L=0.9m,一个质量m=2kg的小物块,置于车的B点,车与小物块均处于静止状态,突然有一质量![]() 的子弹,以速度v=50m/s击中小车并停留在车中,设子弹击中小车的过程时间极短,已知小物块与水平轨道间的动摩擦因数
的子弹,以速度v=50m/s击中小车并停留在车中,设子弹击中小车的过程时间极短,已知小物块与水平轨道间的动摩擦因数![]() ,g取10m/s2则,
,g取10m/s2则,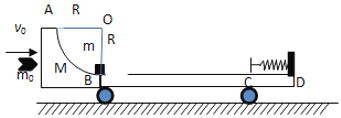
(1)通过计算判断小物块是否能达到圆弧轨道的最高点A,并求当小物块再次回到B点时,小物块的最大速度大小;
(2)若已知弹簧被小物块压缩的最大压缩量x=10cm,求弹簧的最大弹性势能。
【答案】(1)否,5m/s(2)2.5J
【解析】
(1)由于子弹击中小车的过程时间极短,则子弹和小车组成的系统动量守恒,由动量守恒定律求出子弹击中小车后共同速度,此后小物块沿圆轨道上滑,到圆轨道最高点时,子弹、小车和小物块速度相同,由水平动量守恒求出共同速度,再由系统的机械能守恒求小物块上升的最大高度h,将h与R比较,即可判断小物块是否能达到圆弧轨道的最高点A,再根据系统水平动量守恒和机械能守恒求小物块再次回到B点时小物块的最大速度;
(2)当弹簧具有最大弹性势能时三者速度相同,由动量守恒定律和能量守恒定律结合求解;
(1)对于子弹打小车的过程,取向右为正方向,根据动量守恒定律得:![]() ,可得:
,可得:![]()
当小物块运动到圆轨道的最高点时,三者共速为![]() .
.
根据动量守恒定律得:![]() .
.
解得:![]()
根据机械能守恒定律得:![]()
解得:![]() ,所以小物块不能达到圆弧轨道的最高点A;
,所以小物块不能达到圆弧轨道的最高点A;
当小物块再次回到B点时,小物块速度为![]() ,车和子弹的速度为
,车和子弹的速度为![]()
根据动量守恒定律得:![]()
根据能量守恒定律得:![]()
解得![]() ,
,![]() ;
;
(2)当弹簧具有最大弹性势能![]() 时三者速度相同,由动量守恒定律得:
时三者速度相同,由动量守恒定律得:![]() ,可得
,可得 ![]() ;
;
根据能量守恒定律得:![]() .
.
解得:![]() 。
。

【题目】 “用DIS研究加速度与力的关系”的实验装置如图(a)所示,实验中用所挂钩码的重量作为细线对小车的拉力F.通过增加钩码的数量,多次测量,可得小车运动的加速度a和所受拉力F的关系图象.他们在轨道水平和倾斜的两种情况下分别做了实验,得到了两条a﹣F图线,如图(b)所示.

(1)图线 (选填“①”或“②”) 是在轨道右侧抬高成为斜面情况下得到的;
(2)在轨道水平时,小车运动的阻力Ff= N;
(3)(单选)图(b)中,拉力F较大时,a﹣F图线明显弯曲,产生误差.为避免此误差可采取的措施是 .
A.调整轨道的倾角,在未挂钩码时使小车能在轨道上匀速运动 |
B.在增加钩码数量的同时在小车上增加砝码,使钩码的总质量始终远小于小车的总质量 |
C.将无线力传感器捆绑在小车上,再将细线连在力传感器上,用力传感器读数代替钩码的重力 |
D.更换实验中使用的钩码规格,采用质量较小的钩码进行上述实验. |