Question

【题目】如图所示，长木板左端固定一竖直挡板，轻质弹簧左端与挡板连接，右端连接一小物块，在小物块上施加如图所示的水平恒力F，整个系统一起向右在光滑水平面上做匀加速直线运动。已知长木板质量为M，小物块质量为m，弹簧劲度系数为k，形变量为x（x≠0），则（　　）

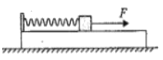
A.小物块的加速度为

B.小物块受到的摩擦力大小一定为

C.小物块受到的摩擦力大小可能为，方向水平向左

D.小物块与长木板之间可能没有摩擦力

Answer 1

【答案】ACD

【解析】

整个系统一起向右在光滑水平面上做匀加速直线运动，对整体，利用牛顿第二定律求加速度，对小物块，根据牛顿第二定律求小物块受到的摩擦力大小，并判断摩擦力方向。

A．对整个系统，由于一起运动，所以小物块的加速度和整体的加速度相同，由牛顿第二定律得小物块的加速度为：

得：

故A正确；

BCD．取水平向右为正方向，假设小物块受到的摩擦力大小为，方向水平向右，若弹簧对小物块的弹力方向水平向右，对小物块，根据牛顿第二定律得：

得：

负号表示方向水平向左，大小为：

若弹簧对小物块的弹力方向水平向左，对小物块，根据牛顿第二定律得：

得：

若：

则，故B错误CD正确。

故选ACD。