题目内容
6. 在如图所示的电路中,电压表和电流表均为理想电表,R2、R3均为定值电阻,且R2=216Ω,R3阻值未知,R1是一滑动变阻器,当其滑片在最左端a时,电压表和电流表示数分别为8V,0.1A;当其滑片在最右端b时,电压表和电流表示数分别为4V,0.5A.求:
在如图所示的电路中,电压表和电流表均为理想电表,R2、R3均为定值电阻,且R2=216Ω,R3阻值未知,R1是一滑动变阻器,当其滑片在最左端a时,电压表和电流表示数分别为8V,0.1A;当其滑片在最右端b时,电压表和电流表示数分别为4V,0.5A.求:(1)电源的电动势和内阻;
(2)定值电阻R3的阻值和滑动变阻器的最大阻值;
(3)电源的最大输出功率.
分析 (1)对滑片在最左端a和最右端b的两种情况,根据闭合电路欧姆定律列式,可求得电源的电动势和内阻.
(2)当滑片在最右端b时,由电压和电流求出R3的阻值.当滑动变阻器滑片滑到最左端a时,根据电路中电流关系列式,可求得滑动变阻器的最大阻值.
(3)根据闭合电路欧姆定律和功率公式结合得到电源的输出功率与电流的关系,再由数学知识求解.
解答 解:(1)由闭合电路欧姆定律可知:
滑片在最左端a时有:Ua=E-Iar,代入得:8=E-0.1×r
滑片在最左端b时有:Ub=E-Iabr,代入得:4=E-0.5×r
解得:E=9V,r=10Ω
(2)当滑动变阻器滑片滑到最右端时,满足:R3=$\frac{{U}_{b}}{{I}_{b}}$=$\frac{4}{0.5}$=8Ω
当滑动变阻器滑片滑到最左端时,满足 Ua=U并+IaR3
且有 $\frac{{U}_{并}}{{R}_{滑}}$+$\frac{{U}_{并}}{{R}_{2}}$=Ia
得:滑动变阻器的最大阻值 R滑=108Ω
(3)【方法一】:路端电压为:U=E-Ir=9-10I
电源的输出功率:P=UI=-10I2+9I
由此可知:当I=-$\frac{b}{2a}$=-$\frac{9}{2×(-10)}$A=0.45A时,取电源的输出功率最大,为 Pm=-10×0.452+9×0.45≈2W
【方法二】:外电阻的范围为:80Ω≥R总≥8Ω,而内电阻r=10Ω在此范围内.
则当R外=r=10Ω时,电源的输出功率最大.
P出max=$\frac{{E}^{2}}{4r}$=2.025W≈2.0W
答:
(1)电源的电动势是9V,内阻是10Ω;
(2)定值电阻R3的阻值是8Ω,滑动变阻器的最大阻值是108Ω;
(3)电源的最大输出功率是2W.
点评 根据两种情况下路端电压和电流,由闭合电路欧姆定律求电源的电动势和内阻是常用的方法,要熟练掌握.对于极值问题,可运用数学上函数法解答.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案| A. | 点电荷是理想模型 | |
| B. | 实际存在的电荷都是点电荷 | |
| C. | 大的带电体不能看成是点电荷 | |
| D. | 点电荷所带的电荷量一定是1.60×10-19C |
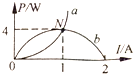 如图所示,抛物线a、b分别是纯电阻直流电路中,内、外电路消耗的电功率随电流变化的图线,N点为抛物线a、b的交点.由该图可知下列说法中正确的是( )
如图所示,抛物线a、b分别是纯电阻直流电路中,内、外电路消耗的电功率随电流变化的图线,N点为抛物线a、b的交点.由该图可知下列说法中正确的是( )| A. | 电源的电动势为8V | |
| B. | 电源的内电阻为4Ω | |
| C. | N点对应外电阻大小为2Ω | |
| D. | 电源被短路时,电源提供的总功率为16W |
 四个相同的小量程电流表分别改装成两个电流表和两个电压表.已知电流表A1量程大于A2的量程,电压表V1的量程大于V2的量程,改装好后把它们按如图所示接入电路,则( )
四个相同的小量程电流表分别改装成两个电流表和两个电压表.已知电流表A1量程大于A2的量程,电压表V1的量程大于V2的量程,改装好后把它们按如图所示接入电路,则( )| A. | 电流表A1的读数小于电流表A2的读数 | |
| B. | 电流表A1的指针偏转角等于电流表A2的指针偏转角 | |
| C. | 电压表V1的读数大于电压表V2的读数 | |
| D. | 电压表V1的指针偏转角大于电压表V2的指针偏转角 |

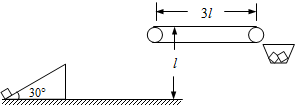
 下图是改装并校准电流表的电路图,已知表头
下图是改装并校准电流表的电路图,已知表头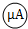 的量程为Ig=600μA、内阻为Rg,
的量程为Ig=600μA、内阻为Rg,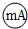 是标准电流表,要求改装后的电流表量程为I=60mA.完成下列填空.
是标准电流表,要求改装后的电流表量程为I=60mA.完成下列填空.