题目内容
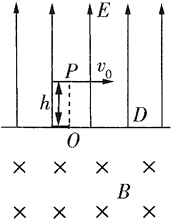 根据载人航天工程第二步任务规划,中国将在2010年至2015年问发射“天宫一号”目标飞行器和“天宫二号”、“天宫三号”两个空间实验室,2020年前后,中国将发射空间站核心舱和科学实验舱,开始建造空间站.假设该空间站体积很大,宇航员可以在里面进行多项体育活动,一宇航员在站内玩垒球(万有引力可以忽略不计),上半侧为匀强电场,下半侧为匀强磁场,中间为分界面,电场与分界面垂直,磁场垂直纸面向里,电场强度为E=100V/m,宇航员位于电场一侧距分界面为h=3m的P点,PO垂直于分界面,点D位于O点右侧,垒球质量为m=0.1kg、带电荷量为q=-0.05C,该宇航员从P点以初速度v0=10m/s平行于分界面投出垒球,要使垒球第一次通过界面就击中D点,且能回到P点.求:
根据载人航天工程第二步任务规划,中国将在2010年至2015年问发射“天宫一号”目标飞行器和“天宫二号”、“天宫三号”两个空间实验室,2020年前后,中国将发射空间站核心舱和科学实验舱,开始建造空间站.假设该空间站体积很大,宇航员可以在里面进行多项体育活动,一宇航员在站内玩垒球(万有引力可以忽略不计),上半侧为匀强电场,下半侧为匀强磁场,中间为分界面,电场与分界面垂直,磁场垂直纸面向里,电场强度为E=100V/m,宇航员位于电场一侧距分界面为h=3m的P点,PO垂直于分界面,点D位于O点右侧,垒球质量为m=0.1kg、带电荷量为q=-0.05C,该宇航员从P点以初速度v0=10m/s平行于分界面投出垒球,要使垒球第一次通过界面就击中D点,且能回到P点.求:(1)OD之间的距离d.
(2)垒球从抛出到第一次回到P点的时间t.(计算结果保留三位有效数字)
分析:(1)垒球在电场中的运动为平抛运动,由平抛运动的规律可得出OD间的距离及在电场中运动的时间;
(2)垒球在磁场中做圆周运动,由几何关系可得出粒子半径的表达式,则由牛顿第二定律可求得B,再由转过的角度可求得在磁场中的转动时间,则可求得总时间.
(2)垒球在磁场中做圆周运动,由几何关系可得出粒子半径的表达式,则由牛顿第二定律可求得B,再由转过的角度可求得在磁场中的转动时间,则可求得总时间.
解答:解:(1)设垒球在电场中运动的加速度大小为a,时间为t1,OD=d则:
由牛顿第二定律,a=
运动学公式,h=
at12
d=v1t
解得:a=50m/s2,
t1=
s,
d=2
m=3.46m
即O、D两点之间的距离为3.46m.
(2)垒球的运动轨迹如图所示.

由图可知,tanθ=
=
,
速度大小为:v=
=20m/s
设垒球作匀速圆周运动半径为R,磁感应强度大小为B,则R=
=4m
根据牛顿第二定律,有:qvB=m
解得B=
=10T
垒球在磁场中运动的时间为:t2=
×
=
s
垒球从抛出到第一次回到P点的时间为:t=2t1+t2=
s=1.53s;
答:(1)OD之间的距离3.46m.
(2)垒球从抛出到第一次回到P点的时间1.53s.
由牛顿第二定律,a=
| qE |
| m |
运动学公式,h=
| 1 |
| 2 |
d=v1t
解得:a=50m/s2,
t1=
| ||
| 5 |
d=2
| 3 |
即O、D两点之间的距离为3.46m.
(2)垒球的运动轨迹如图所示.

由图可知,tanθ=
| at1 |
| v1 |
| 3 |
速度大小为:v=
| v1 |
| cosθ |
设垒球作匀速圆周运动半径为R,磁感应强度大小为B,则R=
| d |
| sinθ |
根据牛顿第二定律,有:qvB=m
| v2 |
| R |
解得B=
| mv |
| qR |
垒球在磁场中运动的时间为:t2=
| 360°-2×60° |
| 360° |
| 2πm |
| qB |
| 4π |
| 15 |
垒球从抛出到第一次回到P点的时间为:t=2t1+t2=
6
| ||
| 15 |
答:(1)OD之间的距离3.46m.
(2)垒球从抛出到第一次回到P点的时间1.53s.
点评:带电粒子在磁场中的转动问题要注意通过分析画出相应的运动图象,由图象即可得出半径关系,再由洛仑兹力充当向心力即可求出待求的磁感应强度,即半径是此类题型的突破口.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目