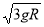题目内容
9. 在长度为L的细线的下端拴一个质量为m的小球,捏住细线的上端,使小球在水平面内做半径为R的匀速圆周运动,试求:
在长度为L的细线的下端拴一个质量为m的小球,捏住细线的上端,使小球在水平面内做半径为R的匀速圆周运动,试求:①小球所受的向心力的大小;
②绳受到的拉力大小;
③小球向心加速度的大小;
④小球做圆周运动的角速度的大小;
⑤小球做圆周运动的线速度的大小.
分析 ①、②小球在水平面内做匀速圆周运动,对小球受力分析,根据合力提供向心力,求出细线拉力的大小.
③根据向心力公式结合几何关系求出向心加速度.
④由向心力公式得:mgtanθ=mω2r,求解角速度大小.
⑤由v=rω,求线速度的大小.
解答  解:①小球在水平面内做匀速圆周运动,对小球受力分析,如图
解:①小球在水平面内做匀速圆周运动,对小球受力分析,如图
小球受重力、和绳子的拉力,合力提供向心力,则向心力 Fn=mgtanθ=mg•$\frac{a}{\sqrt{{l}^{2}-{a}^{2}}}$
②根据几何关系可知:绳受到的拉力大小 T=$\frac{mg}{cosθ}$=mg$\frac{l}{\sqrt{{l}^{2}-{a}^{2}}}$
③由向心力公式得:mgtanθ=ma,
解得:a=gtanθ=$\frac{ag}{\sqrt{{l}^{2}-{a}^{2}}}$
④由向心力公式得:mgtanθ=mω2a
解得:ω=$\sqrt{\frac{g}{lcosθ}}$=$\sqrt{\frac{g}{\sqrt{{l}^{2}-{a}^{2}}}}$
⑤小球做圆周运动的线速度的大小 v=ωa=a$\sqrt{\frac{g}{\sqrt{{l}^{2}-{a}^{2}}}}$
答:
①小球所受的向心力的大小为mg•$\frac{a}{\sqrt{{l}^{2}-{a}^{2}}}$;
②绳受到的拉力大小为mg$\frac{l}{\sqrt{{l}^{2}-{a}^{2}}}$;
③小球向心加速度的大小为$\frac{ag}{\sqrt{{l}^{2}-{a}^{2}}}$;
④小球做圆周运动的角速度的大小$\sqrt{\frac{g}{\sqrt{{l}^{2}-{a}^{2}}}}$;
⑤小球做圆周运动的线速度的大小为a$\sqrt{\frac{g}{\sqrt{{l}^{2}-{a}^{2}}}}$.
点评 本题是圆锥摆问题,关键是分析受力情况,确定向心力的来源.要注意小球圆周运动的半径不等于绳长.

 阅读快车系列答案
阅读快车系列答案
| A. | 绳的拉力等于A的重力 | B. | 绳的拉力小于A的重力 | ||
| C. | 拉力先大于重力,后变为小于重力 | D. | 绳的拉力大于A的重力 |
 一物块在外力作用下沿光滑水平面运动时,其速度与时间的关系如图所示,则下列叙述正确的是 ( )
一物块在外力作用下沿光滑水平面运动时,其速度与时间的关系如图所示,则下列叙述正确的是 ( )| A. | 在O~t1时间内,外力对物块做功的功率逐渐增大 | |
| B. | 在t1~t2时间内,外力对物块做正功 | |
| C. | 在t2~t3时间内,外力对物块做正功 | |
| D. | 在t3时刻,外力对物块做功的功率最大 |
| A. | $\frac{Φ}{S}$ | B. | $\frac{E}{Lv}$ | C. | $\frac{F}{IL}$ | D. | $\sqrt{\frac{FR}{{L}^{2}v}}$ |
 质量为2kg的物体放在光滑水平面上,受到水平方向的恒定拉力的作用,从静止开始经3s速度达到6m/s.求:
质量为2kg的物体放在光滑水平面上,受到水平方向的恒定拉力的作用,从静止开始经3s速度达到6m/s.求: 如图,某星球自转周期为T,飞行器P对此星球执行观测任务,经调整高度,飞行器只受万有引力绕该星球做匀速圆周运动,且相对星球表面静止,测得星球相对飞行器的张角为θ=60°,飞行器正对星球表面发射电磁波经过t时间收到返回信号,已知电磁波在真空中传播速度为C,忽略星球表面大气对电磁波速的影响,求:
如图,某星球自转周期为T,飞行器P对此星球执行观测任务,经调整高度,飞行器只受万有引力绕该星球做匀速圆周运动,且相对星球表面静止,测得星球相对飞行器的张角为θ=60°,飞行器正对星球表面发射电磁波经过t时间收到返回信号,已知电磁波在真空中传播速度为C,忽略星球表面大气对电磁波速的影响,求:

 .轨道底端水平并与半球顶端相切,质量为m的小球由A点静止滑下,最后落在水平面上的C点.重力加速度为g,则( )
.轨道底端水平并与半球顶端相切,质量为m的小球由A点静止滑下,最后落在水平面上的C点.重力加速度为g,则( )