题目内容
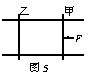
两根平行的金属导轨,固定在同一水平面上,磁感应强度B=0.50T的匀强磁场与导轨平面垂直,导轨电阻不计.导轨间的距离L=0.20m.两根质量均为m=0.10kg的平行金属杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的电阻为R=0.50Ω.如图5所示.在t=0时刻,两杆处于静止状态.现有一与导轨平行、大小为0.20N的恒力F作用于金属杆甲上,使金属杆在导轨上滑动.经过t=5.0s,金属杆甲的加速度为a=1.37m/s2,问此时两金属杆的速度各为多少?
见分析
【试题分析】
在甲开始向右做加速运动的同时,在安培力作用下,乙也开始向右做加速运动.经受力分析可知,二者加速度不同,因此有速度差异,为等长双杆切割型.设任一时刻t两金属杆甲、乙的速度分别为v1、v2,且v1>v2.
闭合回路的感应电动势为E=BL(v1-v2),回路中的电流为
I=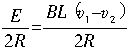 ①
①
对杆甲受力分析如图6所示,
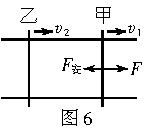
其中F安=BLI.对杆甲有
F-BLI=ma ②
由于作用在杆甲和杆乙的安培力总是大小相等、方向相反,由物体组的动量定理可知两杆的动量增量等于外力F的冲量
Ft=mv1+mv2③
联立①②③式求解得
v1=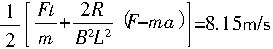
v2=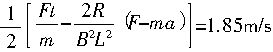
]

练习册系列答案
相关题目
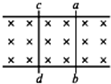 在匀强磁场中有两根平行的金属导轨,磁场方向与导轨平面垂直,导轨上有两根可沿导轨平动的导体棒ab、cd,如图所示,两根导体棒匀速移动的速率分别为v1和v2,则下列情况可以使回路中产生感应电流的是( )
在匀强磁场中有两根平行的金属导轨,磁场方向与导轨平面垂直,导轨上有两根可沿导轨平动的导体棒ab、cd,如图所示,两根导体棒匀速移动的速率分别为v1和v2,则下列情况可以使回路中产生感应电流的是( )| A、ab、cd均向右运动,且v1=v2 | B、ab、cd均向右运动,且v1>v2 | C、ab、cd均向左运动,且v1>v2 | D、ab向右运动,cd向左运动,且v1=v2 |
 如图所示,水平面上放置两根平行的金属导轨,其上面搁置两根可在导轨上自由滑动的金属棒ab和cd,现有一条形磁铁竖直插入ab和cd棒之间,则ab和cd棒的运动情况是( )
如图所示,水平面上放置两根平行的金属导轨,其上面搁置两根可在导轨上自由滑动的金属棒ab和cd,现有一条形磁铁竖直插入ab和cd棒之间,则ab和cd棒的运动情况是( )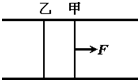 (2003?天津)两根平行的金属导轨,固定在同一水平面上,磁感B=0.50T的匀强磁场与导轨所在平面垂直,导轨的电阻很小,可不计.导轨间的距离l=0.20m.两根质量均为m=0.10kg的平行杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的为电阻R=0.50Ω,在t=0时刻,两杆都处于静止状态.现有一与导轨平行,大小为0.20N的作用于金属杆甲上,使金属杆在导轨上滑动.经过t=0.5s,金属杆甲的加速度a=1.37m/s2,问此时两金属杆的速度各为多少?
(2003?天津)两根平行的金属导轨,固定在同一水平面上,磁感B=0.50T的匀强磁场与导轨所在平面垂直,导轨的电阻很小,可不计.导轨间的距离l=0.20m.两根质量均为m=0.10kg的平行杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的为电阻R=0.50Ω,在t=0时刻,两杆都处于静止状态.现有一与导轨平行,大小为0.20N的作用于金属杆甲上,使金属杆在导轨上滑动.经过t=0.5s,金属杆甲的加速度a=1.37m/s2,问此时两金属杆的速度各为多少? 如图所示,矩形线框abcd可以在两根平行的金属导轨MN.PQ上滑动,把它们放在磁场中,当线框向右滑动时,下列说法哪个正确?( )
如图所示,矩形线框abcd可以在两根平行的金属导轨MN.PQ上滑动,把它们放在磁场中,当线框向右滑动时,下列说法哪个正确?( ) 一个闭合铁心上有初级和次级两个线圈,每组线圈上各连接两根平行的金属导轨,在两组导轨上各放置一根可沿导轨滑动的金属棒L1和L2,垂直导轨平面存在着磁感强度分别为B1、B2的匀强磁场,磁场的方向和线圈的绕向如图所示.金属棒与导轨均接触良好.那么下面说法中正确的是( )
一个闭合铁心上有初级和次级两个线圈,每组线圈上各连接两根平行的金属导轨,在两组导轨上各放置一根可沿导轨滑动的金属棒L1和L2,垂直导轨平面存在着磁感强度分别为B1、B2的匀强磁场,磁场的方向和线圈的绕向如图所示.金属棒与导轨均接触良好.那么下面说法中正确的是( )