题目内容
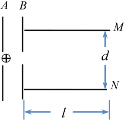
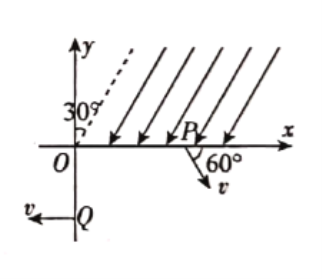
【题目】如图所示，两根相距为L的光滑金属导轨CD、EF固定在水平面内，并处在方向竖直向下的匀强磁场中，导轨足够长且电阻不计。在导轨的左端接入一阻值为R的定值电阻，将质量为m、电阻可忽略不计的金属棒MN垂直放置在导轨上。t=0时刻，MN棒与DE的距离为d，金属棒MN以恒定速度v向右运动过程中；MN棒运动过程中始终与导轨垂直且接触良好，不计空气阻力。
（1）若所加匀强磁场的磁感应强度为B且保持不变，请根据法拉第电磁感应定律E=
推导金属棒MN中的感应电动势E=BLv；
（2）若从t=0时刻起，所加的匀强磁场的磁感应强度B从B0开始逐渐减小时，恰好使回路中不产生感应电流，试从磁通量的角度分析磁感应强度B的大小随时间t的变化规律。
【答案】（1）推导过程见解析 （2）
【解析】
(1) ab棒做匀速直线运动在t时间内的位移为:
线框的面积变化量是：
则穿过闭合电路的磁通量的变化量是：
根据法拉第电磁感应定律得：
(2)由产生感应电流的条件可知，回路中不产生感应电流，则穿过回路的磁通量不变，
根据磁通量不变，应有：
解得：
通城学典默写能手系列答案
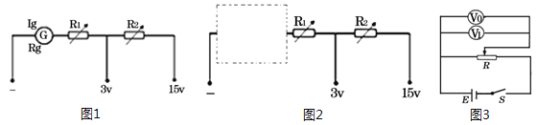
金牌教辅培优优选卷期末冲刺100分系列答案
【题目】如图甲是利用两个电流表A1和A2测量干电池电动势E和内阻r的电路原理图。图中S为开关，R为滑动变阻器，固定电阻R1和A1内阻之和为10000Ω（比r和滑动变阻器的总电阻大得多），A2为理想电流表。
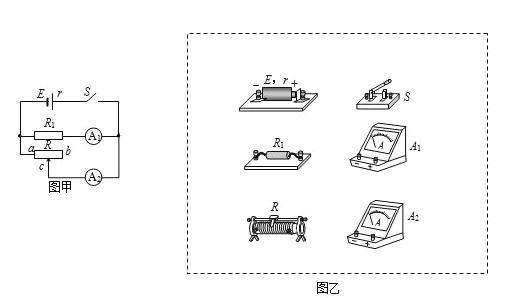
（1）按电路原理图在图乙虚线框内各实物图之间画出连线。（________）
（2）在闭合开关S前，将滑动变阻器的滑动端c移动至________（选填“a端”、“中央”或“b端”）。
（3）闭合开关S，移动滑动变阻器的滑动端c至某一位置，读出电流表A1和A2的示数I1和I2.多次改变滑动端c的位置，得到的数据为
I1/mA | 0.120 | 0.125 | 0.130 | 0.135 | 0.140 | 0.145 |
I1/mA | 480 | 400 | 320 | 232 | 140 | 68 |
在如图所示的坐标纸上以I1为纵坐标、I2为横坐标画出所对应的I1－I2曲线。（________）
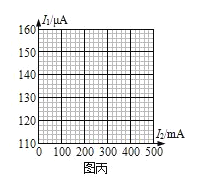
（4）利用所得曲线求得电源的电动势E＝______V，内阻r＝______Ω。（保留两位小数）
（5）该电路中电源输出的短路电流Im＝________A。
