题目内容
【题目】如图,固定在水平面上组合轨道,由光滑的斜面、光滑的竖直半圆(半径R=2.5m)与粗糙的水平轨道组成;水平轨道摩擦因数μ=0.25,与半圆的最低点相切,轨道固定在水平面上.一个质量为m=0.1kg的小球从斜面上A处静止开始滑下,并恰好能到达半圆轨道最高点D,且水平抛出,落在水平轨道的最左端B点处.不计空气阻力,小球在经过斜面与水平轨道连接处时不计能量损失,g取10m/s2.求:
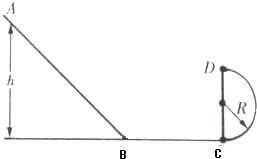
(1)小球出D点的速度v;
(2)水平轨道BC的长度x;
(3)小球开始下落的高度h.
【答案】(1)5m/s;
(2)5m;
(3)7.5m
【解析】
试题分析:(1)小球恰好能到达半圆轨道最高点D,此时只有重力作为向心力,根据向心力的公式可以求出速度的大小;
(2)小球从D点开始做的是平抛运动,水平轨道BC的长度即为平抛运动的水平位移的大小;
(3)对全过程利用动能定理可以求得小球开始下落的高度h.
解:(1)小球恰好能到达半圆轨道最高点D,此时只有重力作为向心力,
即mg=m![]()
所以小球出D点的速度v=![]() =
=![]() =5m/s;
=5m/s;
(2)根据竖直方向上的自由落体运动可得,
2R=![]() gt2,
gt2,
所以运动的时间为t=![]() =
=![]() s=1s,
s=1s,
水平轨道BC的长度即为平抛运动的水平位移的大小,
所以x=vt=5×1=5m.
(3)对从A到D的过程,利用动能定理可得,
mgh﹣μmgx﹣mg2R=![]() m
m![]()
解得h=7.5m
答:(1)小球出D点的速度v为5m/s;
(2)水平轨道BC的长度x为5m;
(3)小球开始下落的高度h为7.5m.

练习册系列答案
相关题目