题目内容
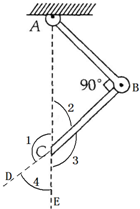 如图所示,一根均匀细棒,上端A处用一铰链与天花板相连,下端B用一铰链与另一均匀细棒相连,两棒的长度相等.两棒在图示的竖直面内运动,且不计铰链处的摩擦.当在C端加一个适当的外力(在纸面内)可使两棒平衡在图示的位置处,即两棒间的夹间为90°,且C端正处在A端的正下方.
如图所示,一根均匀细棒,上端A处用一铰链与天花板相连,下端B用一铰链与另一均匀细棒相连,两棒的长度相等.两棒在图示的竖直面内运动,且不计铰链处的摩擦.当在C端加一个适当的外力(在纸面内)可使两棒平衡在图示的位置处,即两棒间的夹间为90°,且C端正处在A端的正下方.(1)不管两棒质量如何,此外力只可能在哪个范围?(用图中序号表示);
(2)如果AB棒的质量m1=1.0千克,BC棒的质量m2=2.0千克,求此外力的大小和方向.
分析:(1)对两个棒整体受力分析,根据力矩平衡条件确定拉力F的范围;再对杆BC分析,再次根据力矩平衡条件确定范围;最后联立得到拉力的范围;
(2)先后对整体和BC杆运用力矩平衡条件列方程,然后联立求解.
(2)先后对整体和BC杆运用力矩平衡条件列方程,然后联立求解.
解答:解:(1)先对两个棒整体受力分析,重力要事情绕A带你顺时针转动,故拉力F只可能在范围2与3内;
再对杆BC分析,重力要使其逆时针转动,故拉力F只可能在范围1与2内;
综上,拉力只能在范围2内;
(2)设拉力F与AC方向成θ角,根据力矩平衡条件,有:
对整体:(m1+m2)g?
sin45°-F?
Lsinθ=0;
对BC杆:m2g?
sin45°-F?Lsin(45°-θ)=0;
联立解得:F≈19N,θ=arctan
;
答:(1)不管两棒质量如何,此外力只可能在范围2;
(2)此外力的大小约为19N,与竖直方向成arctan
角度且斜向右上方.
再对杆BC分析,重力要使其逆时针转动,故拉力F只可能在范围1与2内;
综上,拉力只能在范围2内;
(2)设拉力F与AC方向成θ角,根据力矩平衡条件,有:
对整体:(m1+m2)g?
| L |
| 2 |
| 2 |
对BC杆:m2g?
| L |
| 2 |
联立解得:F≈19N,θ=arctan
| 3 |
| 7 |
答:(1)不管两棒质量如何,此外力只可能在范围2;
(2)此外力的大小约为19N,与竖直方向成arctan
| 3 |
| 7 |
点评:本题关键多次根据力矩平衡条件列式后联立求解,要有一定的数学运算能力.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图所示,一根长L=
如图所示,一根长L=