题目内容
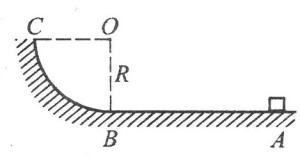
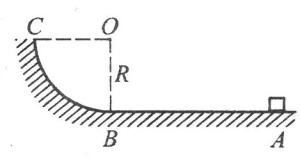
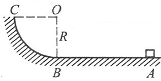 有一质量为m的物体停在摩擦因数μ=0.5的水平面上的A点,在离A为2R的B点有半径为R的1/4光滑圆弧与AB轨道相接,如图所示.现用F=2mg的水平拉力拉物体作加速运动,当物体运动到B时,撤去拉力,求:
有一质量为m的物体停在摩擦因数μ=0.5的水平面上的A点,在离A为2R的B点有半径为R的1/4光滑圆弧与AB轨道相接,如图所示.现用F=2mg的水平拉力拉物体作加速运动,当物体运动到B时,撤去拉力,求:(1)撤去拉力时物体的速度;
(2)在圆弧上运动后能达到的离地的最大高度是多少?
(3)物体最后停在离B点多远的地方?
分析:(1)物体由A到B的过程水平方向受F、摩擦力μmg作用做匀加速直线运动,
应用动能定理或者匀变速直线运动公式均可求解.
(2)对整个过程,运用动能定理列式,求解最大高度.
(3)由机械能守恒定律我们得到物体在光滑圆轨道运动和竖直方向上的运动时没有机械能损失,只有在水平面AB上运动时才有机械能损失;结合摩擦力做功的特点,取整个过程为研究对象,由动能定理得求得总路程S,物体停止的位置找到了.
应用动能定理或者匀变速直线运动公式均可求解.
(2)对整个过程,运用动能定理列式,求解最大高度.
(3)由机械能守恒定律我们得到物体在光滑圆轨道运动和竖直方向上的运动时没有机械能损失,只有在水平面AB上运动时才有机械能损失;结合摩擦力做功的特点,取整个过程为研究对象,由动能定理得求得总路程S,物体停止的位置找到了.
解答:解:(1)根据题意已知在撤去拉力之前,该物体作匀加速直线运动.
根据动能定理得:(F-μmg)2R=
mvB2
所以:vB=
(2)由于圆弧轨道光滑,所以,上冲过程由动能定理得:
-mgh=0-
mvB2
得:h=3R;
(3)当物体再次到B点时,速度大小不变.
之后物体在AB轨道上滑动,此时只有滑动摩擦力做功.
-μmgs=0-
mvB2
解之得:s=6R;
答:
(1)撤去拉力时物体的速度为
;
(2)在圆弧上运动后能达到的离地的最大高度是3R.
(3)物体最后停在离B点6R的地方.
根据动能定理得:(F-μmg)2R=
| 1 |
| 2 |
所以:vB=
| 6gR |
(2)由于圆弧轨道光滑,所以,上冲过程由动能定理得:
-mgh=0-
| 1 |
| 2 |
得:h=3R;
(3)当物体再次到B点时,速度大小不变.
之后物体在AB轨道上滑动,此时只有滑动摩擦力做功.
-μmgs=0-
| 1 |
| 2 |
解之得:s=6R;
答:
(1)撤去拉力时物体的速度为
| 6gR |
(2)在圆弧上运动后能达到的离地的最大高度是3R.
(3)物体最后停在离B点6R的地方.
点评:本题考查动能定理的应用,选取不同的过程为研究对象是解题的关键,是我们列方程的基础,过程选得好往往方程简便易解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
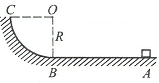 有一质量为m的物体停在摩擦因数μ=0.5的水平面上的A点,在离A为2R的B点有半径为R的
有一质量为m的物体停在摩擦因数μ=0.5的水平面上的A点,在离A为2R的B点有半径为R的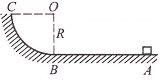 有一质量为m的物体停在动摩擦因数μ=0.5的水平面上的A点,在离A为2R的B点有半径为R的
有一质量为m的物体停在动摩擦因数μ=0.5的水平面上的A点,在离A为2R的B点有半径为R的