题目内容
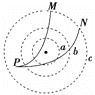
【题目】如图所示,虚线a、b、c为三个同心圆面,圆心处有一个点电荷.现从b、c之间一点P以相同的速率发射两个带电粒子,分别沿PM、PN运动到M、N点,M、N两点都处于圆周c上,以下判断正确的是( )
A. 到达M、N时两粒子速率仍相等
B. 到达M、N时两粒子速率vM>vN
C. 到达M、N时两粒子的电势能相等
D. 两个粒子的电势能都是先减小后增大
【答案】B
【解析】试题分析:根据轨迹的弯曲方向确定带电粒子所受的电场力方向,根据动能定理确定到达M、N时两粒子速率关系.由电场力做功正负分析电势能的变化.
解:AB、由轨迹看出,点电荷左侧的带电粒子受排斥力,右侧的带电粒子受吸引力,由题,M、N两点都处于圆周c上,电势相等,两带电粒子又是从同一点P出发,则电势差UPM=UPN,电场力对两个带电粒子做功大小相等,而从P到M的粒子电场力总功为正功,从P到N的粒子电场力总功为负功,根据动能定理得到,到达M、N时两粒子速率vM>vN.故A错误,B正确.
C、由轨迹看出,点电荷左侧的带电粒子有排斥力,与中心点电荷电性相同;对右侧的带电粒子有吸引力,与中心点电荷电性相反,则两粒子带异种电荷,由公式Ep=qφ知两个粒子到达M、N时电势能不等,故C错误,
D、电场力对左侧的粒子先做负功后做正功,电势能先增大后减小,故D错误.
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目