题目内容
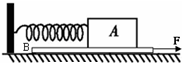 如图所示,A物块的质量为2kg,放在不光滑的水平木板B上,一劲度系数为150N/m的轻弹簧一端连着B,另一端固定,弹簧处于原长.g取10m/s2:
如图所示,A物块的质量为2kg,放在不光滑的水平木板B上,一劲度系数为150N/m的轻弹簧一端连着B,另一端固定,弹簧处于原长.g取10m/s2:(1)现用F=10N水平力向右拉木板B,没拉动,求此状态A物块受到的摩擦力?
(2)增大水平力F使木板从A下方向右抽出,在抽出过程中弹簧伸长了4cm,求此状态A物块受到的摩擦力?
(3)求物块A与木板B之间的动摩擦因数?
分析:(1)根据B的运动情况,来确定A是否受到静摩擦力作用;
(2)根据弹簧的形变,结合胡克定律,依据平衡方程,即可求解A受到的滑动摩擦力;
(3)根据滑动摩擦力公式Ff=μFN,即可求解.
(2)根据弹簧的形变,结合胡克定律,依据平衡方程,即可求解A受到的滑动摩擦力;
(3)根据滑动摩擦力公式Ff=μFN,即可求解.
解答:解:(1)F=10N水平力向右拉木板B,没拉动,A处于静止状态,弹簧没有形变量,则A受到的摩擦力为0;(2)由题意可知,使木板从A下方向右抽出,弹簧伸长了4cm,
根据胡克定律,则有:F弹=k△X
代入数据解得:Ff=F弹=6N
B相对A向右滑行,则A相对B向左滑行,因此A受到的滑动摩擦力方向向右,
(3)对A来说,竖直方向,FN=mg=20N
根据Ff=μFN,则有:?=
=
=0.3
答:(1)此状态A物块受到的摩擦力为零;
(2)此状态A物块受到的摩擦力6N;
(3)物块A与木板B之间的动摩擦因数为0.3.
根据胡克定律,则有:F弹=k△X
代入数据解得:Ff=F弹=6N
B相对A向右滑行,则A相对B向左滑行,因此A受到的滑动摩擦力方向向右,
(3)对A来说,竖直方向,FN=mg=20N
根据Ff=μFN,则有:?=
| Ff |
| FN |
| 6 |
| 20 |
答:(1)此状态A物块受到的摩擦力为零;
(2)此状态A物块受到的摩擦力6N;
(3)物块A与木板B之间的动摩擦因数为0.3.
点评:考查静摩擦力与滑动摩擦力如何区分,及怎样求解静摩擦力方法,注意理解滑动摩擦力公式的应用,当心压力与重力不总是相等.同时掌握胡克定律,注意△X是形变量,而不是弹簧长度.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
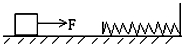 在光滑水平面上有一物块受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触并将弹簧压至最短的过程中,下列说法正确的是( )
在光滑水平面上有一物块受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触并将弹簧压至最短的过程中,下列说法正确的是( )| A、物块接触弹簧后即做减速运动 | B、物块接触弹簧后先加速后减速 | C、当物块的速度为零时,它所受的合力也为零 | D、当物体加速度为零时,物块的速度也等于零 |
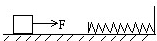 在光滑水平面上有一物块受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触并将弹簧压至最短的过程中,下列说法正确的是( )
在光滑水平面上有一物块受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触并将弹簧压至最短的过程中,下列说法正确的是( ) 在光滑水平面上有一物块始终受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触后向右运动的过程中,下列说法正确的是( )
在光滑水平面上有一物块始终受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触后向右运动的过程中,下列说法正确的是( ) (2010?镇江一模)如图所示,长方体物块C置于水平地面上,物块A、B用不可伸长的轻质细绳通过滑轮连接(不计滑轮与绳之间的摩擦),A物块与C物块光滑接触,整个系统中的A、B、C三物块在水平恒定推力F作用下从静止开始以相同的加速度一起向左运动.下列说法正确的是( )
(2010?镇江一模)如图所示,长方体物块C置于水平地面上,物块A、B用不可伸长的轻质细绳通过滑轮连接(不计滑轮与绳之间的摩擦),A物块与C物块光滑接触,整个系统中的A、B、C三物块在水平恒定推力F作用下从静止开始以相同的加速度一起向左运动.下列说法正确的是( )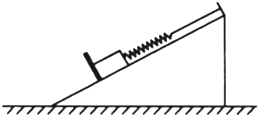 如图所示,某物块静止在光滑斜面上,物块与一轻质弹簧相连,弹簧被固定在斜面的顶端,物块的下端用一个垂直于斜面的挡板挡住,整个装置处于静止状态,则物块的受力个数可能为( )
如图所示,某物块静止在光滑斜面上,物块与一轻质弹簧相连,弹簧被固定在斜面的顶端,物块的下端用一个垂直于斜面的挡板挡住,整个装置处于静止状态,则物块的受力个数可能为( )