题目内容
【题目】如图所示,水平传送带以速度v1=2m/s匀速向左运动,小物体P、Q由通过定滑轮且不可伸长的轻绳相连,mP=2kg、mQ=1kg,小物体P与传送带之间的动摩擦因数μ=0.1.某时刻P在传送带右端具有向左的速度v2=4m/s,P与定滑轮间的绳水平.不计定滑轮质量和摩擦,小物体P与传送带之间的最大静摩擦力等于滑动摩擦力,传送带、绳足够长,取g=10m/s2 . 求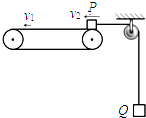
(1)P在传送带上向左运动的最大距离;
(2)P离开传送带时的速度.(结果可用根号表示)
【答案】
(1)解:P先以加速度a1向左做匀减速运动,直到速度减为v1,设位移为x1,由牛顿第二定律得
对p:T1+μmpg=mpa1
对Q:mQg﹣T1=mQa1
联立以上方程解得:a1=4m/s2
由运动学公式得: ![]()
解得:x1=1.5m
p接着以加速度a2向左做匀减速运动,直到速度减为0,设位移为x2,由牛顿第二定律得
对p:T2﹣μmpg=mpa2
对Q:mQg﹣T2=mQa2
联立以上方程解得:a2= ![]() m/s2
m/s2
由运动学公式得: ![]()
解得:x2=0.75m
故P向左运动的最大距离x=x1+x2=2.25m
答:P在传送带上向左运动的最大距离为2.25m;
(2)解:P向左的速度减为0后,再以加速度a2向右做匀加速运动,直到从右端离开传送带,由运动学公式得:
v2=2a2x
解得:v= ![]()
答:P离开传送带时的速度为 ![]() .
.
【解析】P先以加速度a1向左做匀减速运动,直到速度减为v1,接着以加速度a2向左做匀减速运动,直到速度减为0,根据牛顿第二定律和运动学公式即可求解
【考点精析】利用匀变速直线运动的速度、位移、时间的关系对题目进行判断即可得到答案,需要熟知速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值.