题目内容
9.物体静止在光滑水平面上,先施加一水平向右的恒力 F1,经t时间后撤去 F1,立刻施加另一水平向左的恒力 F2,又经t时间后物体回到开始出发点.在前后两段时间内,F1、F2的平均功率为 P1、P2,F1、F2在t时刻和2t时刻的瞬时功率为 P3、P4间的关系是( )| A. | P1=P2 | B. | 3P1=P2 | C. | 3P3=P4 | D. | 6P3=P4 |
分析 物体先做匀加速运动,后做匀减速运动回到原处,整个过程中的位移为零.根据牛顿第二定律和运动学公式即可确定两个力的大小关系,速度的关系可根据运动学速度时间公式求解,平均功率等于功除以时间,瞬时功率等于恒力与瞬时速度的乘积.
解答 解:A、物体从静止起受水平恒力F1 作用,做匀加速运动,经一段时间t后的速度为:v1=a1t=$\frac{{F}_{1}}{m}$t
以后受恒力F2,做匀减速运动,加速度大小为:a2=$\frac{{F}_{2}}{m}$经同样时间后回到原处,整个时间内再联系物体的位移为零,得:
$\frac{1}{2}{a}_{1}{t}^{2}+{v}_{1}t-\frac{1}{2}{a}_{2}{t}^{2}=0$
解得:F1:F2=1:3
又经时间t后物体回到出发点,所以:x1=x2
两个力做的功:W1=F1x1,W2=F2x2
所以$\frac{{P}_{1}}{{P}_{2}}=\frac{\frac{{W}_{1}}{t}}{\frac{{W}_{2}}{t}}=\frac{1}{3}$,故A错误,B正确.
C、F1在t时刻的瞬时功率${P}_{3}={F}_{1}{v}_{1}=\frac{{{F}_{1}}^{2}}{m}t$,
2t时刻的瞬时速度${v}_{2}={v}_{1}-{a}_{2}t=\frac{{F}_{1}}{m}t-\frac{{F}_{2}}{m}t$,
则F2在2t时刻的瞬时功率P4=F2v2=$-\frac{{{6F}_{1}}^{2}}{m}t$,
则6P3=P4,故C错误,D正确.
故选:BD
点评 在F1和F2的作用下,在相同的时间内,物体回到原处,说明位移的大小相同,这是解这道题的关键点,注意平均功率与瞬时功率的区别.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案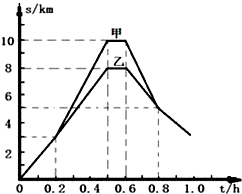 甲乙两人同时同地出发骑自行车做直线运动,前1小时内的位移-时间图象如图所示.下列表述正确的是( )
甲乙两人同时同地出发骑自行车做直线运动,前1小时内的位移-时间图象如图所示.下列表述正确的是( )| A. | 0.2-0.5小时内,甲的加速度比乙的大 | |
| B. | 0.8小时内,甲、乙骑行的路程相等 | |
| C. | 0.6-0.8小时内,甲的位移比乙的小 | |
| D. | 0.2-0.5小时内,甲的速度比乙的大 |
| A. | 速度与位移成正比 | B. | 速度与时间成反比 | ||
| C. | 速度与位移成正比,与时间成反比 | D. | 速度由位移和时间的比值确定 |
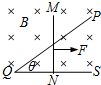 如图所示,固定在水平面上的三角形金属导轨PQS顶角为θ,处于竖直向下的匀强磁场中.一根金属棒MN与金属导轨材料和横截面积相同并放在导轨上,保持MN⊥QS.金属棒MN在水平向右的拉力F作用下向右匀速运动,MN与导轨间的接触电阻和摩擦都忽略不计.则下列说法中正确的是( )
如图所示,固定在水平面上的三角形金属导轨PQS顶角为θ,处于竖直向下的匀强磁场中.一根金属棒MN与金属导轨材料和横截面积相同并放在导轨上,保持MN⊥QS.金属棒MN在水平向右的拉力F作用下向右匀速运动,MN与导轨间的接触电阻和摩擦都忽略不计.则下列说法中正确的是( )| A. | 回路中的感应电流方向为顺时针方向,大小逐渐增大 | |
| B. | 回路中的感应电流方向为逆时针方向,大小逐渐减小 | |
| C. | 回路中的感应电流方向为逆时针方向,大小保持不变 | |
| D. | 水平拉力F的大小保持不变 |
 如图所示,一质量为m的小球在水平细线和与竖直方向成θ角的轻质弹簧作用下处于静止状态则下列说法正确的是( )
如图所示,一质量为m的小球在水平细线和与竖直方向成θ角的轻质弹簧作用下处于静止状态则下列说法正确的是( )| A. | 剪断细线的瞬间小球加速度的大小为gtanθ,方向水平向右 | |
| B. | 剪断细线的瞬间小球加速度的大小为gsinθ,方向与水平方向夹角为θ向右下 | |
| C. | 若将弹簧剪断的瞬间小球加速度的大小为$\frac{g}{cosθ}$,方向与竖直方向夹角为θ向右下 | |
| D. | 若将弹簧剪断的瞬间小球加速度的大小为零 |
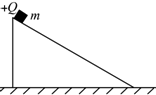 如图所示,倾角为α,表面摩擦因数为μ的斜面固定于地面上(μ<tanα),并处于方向垂直纸面向外、强度为B的匀强磁场中,质量为m、带电量为+Q的小滑块从斜面顶端由静止下滑,在滑块下滑的过程中,下列判断正确的是( )
如图所示,倾角为α,表面摩擦因数为μ的斜面固定于地面上(μ<tanα),并处于方向垂直纸面向外、强度为B的匀强磁场中,质量为m、带电量为+Q的小滑块从斜面顶端由静止下滑,在滑块下滑的过程中,下列判断正确的是( )| A. | 滑块受到的摩擦力不变 | |
| B. | 滑块到达地面时的动能与B的大小有关 | |
| C. | 滑块受到的洛伦兹力方向垂直斜面向下 | |
| D. | 即使B很大滑块也一定会由静止下滑,当最终有可能减速并停在斜面上 |
| A. | 体积很小的物体都可看成质点 | |
| B. | 只有低速运动的物体才可看成质点,高速运动的物体不可看作质点 | |
| C. | 不论物体的质量多大,只要物体的尺寸对所研究的问题没有影响或影响可以不计,就可以看成质点 | |
| D. | 一枚硬币用力上抛,猜测它落地时是正面朝上还是反面朝上,可以将硬币视为质点 |
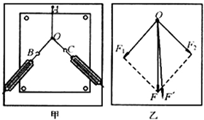 在“探究求合力的方法”的实验情况如图甲所示,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳;先后两次拉伸橡皮条,一次是用两个弹簧测力计通过两细绳互成角度地拉橡皮条,另一次是用一个弹簧测力计通过细绳拉橡皮条.其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
在“探究求合力的方法”的实验情况如图甲所示,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳;先后两次拉伸橡皮条,一次是用两个弹簧测力计通过两细绳互成角度地拉橡皮条,另一次是用一个弹簧测力计通过细绳拉橡皮条.其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.