题目内容
7.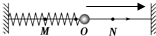 如图所示,一弹簧振子在M、N间沿光滑水平杆做简谐运动,坐标原点O为平衡位置,MN=4cm.从小球图中N点时开始计时,到第一次经过O点的时间为0.1s,则小球振动的周期为0.4s,振动方程的表达式为x=2cos5πtcm,.
如图所示,一弹簧振子在M、N间沿光滑水平杆做简谐运动,坐标原点O为平衡位置,MN=4cm.从小球图中N点时开始计时,到第一次经过O点的时间为0.1s,则小球振动的周期为0.4s,振动方程的表达式为x=2cos5πtcm,.
分析 对于简谐运动,从正向最大位移处开始计时,其位移时间关系公式为:x=Acosωt;第一次经过O点的时间为0.1s,代入公式计算出角频率和周期,再写出振动方程.
解答 解:如图,从正向最大位移处开始计时,振动方程的表达式为为:x=Acosωt;
其中振幅 A=2cm;
据题可得:T=4×0.1s=0.4s,则ω=$\frac{2π}{T}$=5π rad/s
则振动方程的表达式为为:x=2cos5πt cm.
故答案为:0.4,2cos 5πt.
点评 本题关键记住简谐运动的位移时间关系表达式,要能结合时间与周期的关系求解周期.

练习册系列答案
相关题目
17.下列说法说法正确的是( )
| A. | 电场中某点的场强方向跟正电荷在该点所受的电场力的方向相同 | |
| B. | 根据E=$\frac{F}{q}$可知,电场中某点的电场强度与电场力F成正比,与电量q成反比 | |
| C. | E是矢量,与F的方向一致 | |
| D. | 电场线是电荷的运动轨迹 |
15.如果a-$\frac{1}{m}$图象是通过原点的一条直线,则说明( )
| A. | 物体的加速度a与物体的质量m成正比 | |
| B. | 物体的加速度a与物体的质量m成反比 | |
| C. | 物体的质量m与物体的加速度a成正比 | |
| D. | 物体的质量m与物体的加速度a成反比 |
2.图所示是一辆汽车和一辆摩托车同时同地沿同一方向做直线运动的vt图象,则由图象可知( )
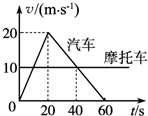

| A. | 40 s末汽车在摩托车之前 | B. | 20 s末汽车运动方向发生改变 | ||
| C. | 60 s内两车相遇两次 | D. | 60 s末汽车回到出发点 |
12.两个电量不同的正离子,被同一电场加速后垂直进入同一偏转电场,下列说法正确的是( )
| A. | 比荷$\frac{q}{m}$大的正离子离开偏转电场时的偏转角大 | |
| B. | 比荷$\frac{q}{m}$大的正离子离开偏转电场时的偏转角小 | |
| C. | 比荷$\frac{q}{m}$不同的正离子离开偏转电场时速度方向相同 | |
| D. | 带电量大的正离子离开偏转电场时的偏转角大 |
19. 如图所示,一物块以速度v1从曲面上A点处下滑,运动到B点处速度大小仍为v1,若物块以速度v2(v2>v1)仍从A点下滑,则运动到B点时速度的大小将( )
如图所示,一物块以速度v1从曲面上A点处下滑,运动到B点处速度大小仍为v1,若物块以速度v2(v2>v1)仍从A点下滑,则运动到B点时速度的大小将( )
 如图所示,一物块以速度v1从曲面上A点处下滑,运动到B点处速度大小仍为v1,若物块以速度v2(v2>v1)仍从A点下滑,则运动到B点时速度的大小将( )
如图所示,一物块以速度v1从曲面上A点处下滑,运动到B点处速度大小仍为v1,若物块以速度v2(v2>v1)仍从A点下滑,则运动到B点时速度的大小将( )| A. | 稍大于v2 | B. | 稍小于v2 | C. | 等于v2 | D. | 无法确定 |
16. 杂技演员在进行“顶杆”表演时,用的是一根质量可忽略不计的长竹竿,表演者自杆顶由静止开始下滑,5s末滑到杆底时速度恰好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,以表演者开始下滑时刻为计时起点,传感器显示的压力随时间变化的情况如图所示,取g=10m/s2,以下说法正确的是( )
杂技演员在进行“顶杆”表演时,用的是一根质量可忽略不计的长竹竿,表演者自杆顶由静止开始下滑,5s末滑到杆底时速度恰好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,以表演者开始下滑时刻为计时起点,传感器显示的压力随时间变化的情况如图所示,取g=10m/s2,以下说法正确的是( )
 杂技演员在进行“顶杆”表演时,用的是一根质量可忽略不计的长竹竿,表演者自杆顶由静止开始下滑,5s末滑到杆底时速度恰好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,以表演者开始下滑时刻为计时起点,传感器显示的压力随时间变化的情况如图所示,取g=10m/s2,以下说法正确的是( )
杂技演员在进行“顶杆”表演时,用的是一根质量可忽略不计的长竹竿,表演者自杆顶由静止开始下滑,5s末滑到杆底时速度恰好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,以表演者开始下滑时刻为计时起点,传感器显示的压力随时间变化的情况如图所示,取g=10m/s2,以下说法正确的是( )| A. | 该表演者下滑的最大速度为2.4m/s | |
| B. | 该表演者的质量为50kg | |
| C. | 竹竿的总长度为6.0m | |
| D. | 该表演者下滑过程中,0-1s内处于超重状态,1-5s内处于失重状态 |
17. 如图所示,在等量异种电荷形成的电场中,有A、B、C三点,A为两点荷连线的中心,B为连线上距A为d的一点,C为连线中垂上距A也为d的一点,关于三点的场强大小、电势高低比较,一负电荷在这三点的电势能分别为EPA,EPB,EPC.正确的是( )
如图所示,在等量异种电荷形成的电场中,有A、B、C三点,A为两点荷连线的中心,B为连线上距A为d的一点,C为连线中垂上距A也为d的一点,关于三点的场强大小、电势高低比较,一负电荷在这三点的电势能分别为EPA,EPB,EPC.正确的是( )
 如图所示,在等量异种电荷形成的电场中,有A、B、C三点,A为两点荷连线的中心,B为连线上距A为d的一点,C为连线中垂上距A也为d的一点,关于三点的场强大小、电势高低比较,一负电荷在这三点的电势能分别为EPA,EPB,EPC.正确的是( )
如图所示,在等量异种电荷形成的电场中,有A、B、C三点,A为两点荷连线的中心,B为连线上距A为d的一点,C为连线中垂上距A也为d的一点,关于三点的场强大小、电势高低比较,一负电荷在这三点的电势能分别为EPA,EPB,EPC.正确的是( )| A. | EB>EA>EC | B. | EPA﹦EPB<EPC | C. | UA=UC>UB | D. | UB=UC>UA |
 如图所示,设A、B为地球赤道圆的一条直径的两端,利用同步卫星将一电磁波信号由A点传到B点,已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对电磁波的折射.设电磁波在空气中的传播速度为c.求:
如图所示,设A、B为地球赤道圆的一条直径的两端,利用同步卫星将一电磁波信号由A点传到B点,已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对电磁波的折射.设电磁波在空气中的传播速度为c.求: