题目内容
 (2004?杭州一模)一条长为L的细线,上端固定,下端拴一质量为m的带电小球,将它置于一匀强电场中,电场强度大小为E,方向水平.已知当细线离开竖直位置的偏角为α时,小球处于平衡如图所示,问:
(2004?杭州一模)一条长为L的细线,上端固定,下端拴一质量为m的带电小球,将它置于一匀强电场中,电场强度大小为E,方向水平.已知当细线离开竖直位置的偏角为α时,小球处于平衡如图所示,问:(1)小球带何种电?
(2)小球所带的电量是多少?
(3)如果细线的偏角由α增大到φ,然后将小球由静止开始释放,则φ应为多大时才能使细线到竖直位置时,小球的速度刚好为零?
分析:(1)小球在电场中受到重力、电场力和细线的拉力而处于平衡状态.根据细线偏离的方向,分析电场力方向,确定小球的电性.
(2)根据平衡条件和电场力公式F=qE,列方程求出小球所带的电量.
(3)将细线的偏角由α向右增大到90°,由静止开始释放后,根据动能定理求出小球运动到悬点正下方时的速度,再由牛顿第二定律求出绳上的拉力.
(2)根据平衡条件和电场力公式F=qE,列方程求出小球所带的电量.
(3)将细线的偏角由α向右增大到90°,由静止开始释放后,根据动能定理求出小球运动到悬点正下方时的速度,再由牛顿第二定律求出绳上的拉力.
解答:解: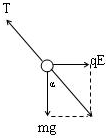 (1)由图可知,小球所受电场力方向水平向右,场强也水平向右,则小球带正电荷.
(1)由图可知,小球所受电场力方向水平向右,场强也水平向右,则小球带正电荷.
(2)以小球为研究对象,分析受力,作出力图如图.根据平衡条件得
qE=mgtanα
得到:q=
tanα
(3)将细线的偏角由α向右增大到φ,由静止开始释放后,小球运动到到悬点正下方位置时速度为O,根据动能定理得
mgL(1-cosφ)-qELsinφ=0-0
又qE=mgtanα
sin2φ+cos2φ=1
联立以上各式,整理得到:tan
=tanα,所以:φ=2α
答:(1)小球带正电荷.
(2)小球所带的电量是q=
tanα.
(3)则φ应为2α时才能使细线到竖直位置时,小球的速度刚好为零.
 (1)由图可知,小球所受电场力方向水平向右,场强也水平向右,则小球带正电荷.
(1)由图可知,小球所受电场力方向水平向右,场强也水平向右,则小球带正电荷.(2)以小球为研究对象,分析受力,作出力图如图.根据平衡条件得
qE=mgtanα
得到:q=
| mg |
| E |
(3)将细线的偏角由α向右增大到φ,由静止开始释放后,小球运动到到悬点正下方位置时速度为O,根据动能定理得
mgL(1-cosφ)-qELsinφ=0-0
又qE=mgtanα
sin2φ+cos2φ=1
联立以上各式,整理得到:tan
| φ |
| 2 |
答:(1)小球带正电荷.
(2)小球所带的电量是q=
| mg |
| E |
(3)则φ应为2α时才能使细线到竖直位置时,小球的速度刚好为零.
点评:本题整合了物体的平衡、牛顿第二定律和动能定理等多个规律,分析受力是基础,要培养分析受力情况、作力图的习惯.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (2004?杭州一模)欲测电阻R的阻值,现有几个标准电阻,一个电池和一只未经标定的电流计,连成如图所示的电路,第一次与电流计并联的电阻为r1=50Ω,电流计的示度为3.9格,第二次改用r2=100Ω,电流计的示度为5.2格,第三次改用r3=10Ω,同时将待测电阻R换成一个R′=20kΩ标准电阻,结果电流计的示度为7.8格,已知电流计的示度与所通过的电流成正比,求电阻R的阻值.
(2004?杭州一模)欲测电阻R的阻值,现有几个标准电阻,一个电池和一只未经标定的电流计,连成如图所示的电路,第一次与电流计并联的电阻为r1=50Ω,电流计的示度为3.9格,第二次改用r2=100Ω,电流计的示度为5.2格,第三次改用r3=10Ω,同时将待测电阻R换成一个R′=20kΩ标准电阻,结果电流计的示度为7.8格,已知电流计的示度与所通过的电流成正比,求电阻R的阻值. (2004?杭州一模)用电子射线管演示带电粒子的磁场中受洛仑兹力的实验装置如图所示,图中虚线是带电粒子的运动轨迹,那么A接直流高压电源的
(2004?杭州一模)用电子射线管演示带电粒子的磁场中受洛仑兹力的实验装置如图所示,图中虚线是带电粒子的运动轨迹,那么A接直流高压电源的