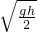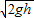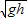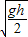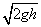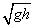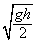Question

从距地面高h的台子上自由落下的石块A，同时在石块A的正下方的地面处，以初速度v₀把石块B竖直向上抛出，不计空气阻力，则A、B在空中可以相遇的条件是（　　）

• A．v₀＞

  2gh

• B．v₀＞

  gh

• C．v₀＞

  gh 2

• D．无法确定

Answer 1

分析：石块A做自由落体运动，石块B做竖直上抛运动；根据位移时间公式分别求出甲和乙的位移大小，两物体在空中相碰，知两物体的位移之和等于h，再结合相遇的时间小于乙落地的时间，求出乙的初速度v₀应满足的条件．

解答：解：设经过时间t甲乙在空中相碰，甲做自由落体运动的位移
h₁=

1

2

gt²  ①
乙做竖直上抛运动的位移 h₂=v₀t-

1

2

gt²  ②
由几何关系 h=h₁+h₂     ③
联立①②③解得 t=

h

v0

    ④
设乙抛出后经过时间t_max落地，根据速度-时间关系有 t_max=

2v0

g

    ⑤
甲乙在空中相遇应满足 0＜t＜t_max ⑥
联立④⑤⑥解得 v₀≥

gh 2

故选C．

点评：解决本题的关键知道两物体在空中相碰，两物体的位移之和等于h，结合物体运动时间的范围，求出初始度的范围．