题目内容
19.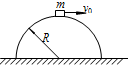 一个质量为m的物体(体积可忽略)在半径为R的光滑半球面顶点处以水平速度v0运动.如图所示,则下列结论中正确的是( )
一个质量为m的物体(体积可忽略)在半径为R的光滑半球面顶点处以水平速度v0运动.如图所示,则下列结论中正确的是( )| A. | 若v0=0,则物体m对半球面顶点的压力为0 | |
| B. | 若v0=2$\sqrt{gR}$则物体m在半球面顶点下方的某个位置会离开半球面 | |
| C. | 若v0=$\sqrt{gR}$,则物体m对半球面顶点的压力为mg | |
| D. | 若v0=$\frac{1}{2}$$\sqrt{gR}$,则物体m对半球面顶点的压力为$\frac{3}{4}$mg |
分析 在最高点,物体沿半径方向的合力提供向心力,根据牛顿第二定律判断是否有支持力,从而判断物体的运动情况
解答 解:A、设物体受支持力为F,根据牛顿第二定律:mg-F=m$\frac{{v}_{0}^{2}}{R}$=0,得:F=mg,根据牛顿第三定律物体对半球面顶点的压力大小等于mg,故A错误;
C、若v0=$\sqrt{gR}$,则mg-F=m$\frac{{v}_{0}^{2}}{R}$,得:F=0,则物体对半球面顶点无压力,故C错误;
B、若v≥$\sqrt{gR}$时,F=0,物体在顶部仅受重力,有水平初速度,做平抛运动,即若v0=2$\sqrt{gR}$,则物体经过最高点后立即离开半球面,故B错误;
D、若v0=$\frac{1}{2}$$\sqrt{gR}$,则mg-F=m$\frac{{{v}_{0}}^{2}}{R}$,得:F=$\frac{3}{4}mg$,则物体对半球面顶点的压力为$\frac{3}{4}$mg,故D正确;
故选:D
点评 解决本题的关键知道物体做圆周运动向心力的来源,以及知道平抛运动的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.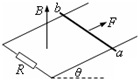 如图所示,两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻不计,磁场方向垂直于斜面向上,质量为m、电阻不计的金属棒ab在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑h高度,在此过程中( )
如图所示,两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻不计,磁场方向垂直于斜面向上,质量为m、电阻不计的金属棒ab在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑h高度,在此过程中( )
 如图所示,两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻不计,磁场方向垂直于斜面向上,质量为m、电阻不计的金属棒ab在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑h高度,在此过程中( )
如图所示,两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻不计,磁场方向垂直于斜面向上,质量为m、电阻不计的金属棒ab在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑h高度,在此过程中( )| A. | 作用于金属棒上的各个力的合力所做的功等于零 | |
| B. | 作用于金属棒上的各个力的合力所做的功等于mgh与电阻R上发出的焦耳热之和 | |
| C. | 恒力F与安培力的合力所的功等于零 | |
| D. | 恒力F与安培力的合力所做的功等于电阻R上发出的焦耳热 |
10.如图所示,洗衣机的脱水桶采用带动衣物旋转的方式脱水,下列说法中正确的是( )

| A. | 水会从桶中甩出是因为水滴受到的力突然消失了 | |
| B. | 水会从桶中甩出是因为水滴受到向心力很大的缘故 | |
| C. | 加快脱水桶转动角速度,脱水效果会更好 | |
| D. | 这是一种离心现象的应用 |
7.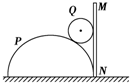 半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止,则在此过程中,下列说法正确的是( )
半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止,则在此过程中,下列说法正确的是( )
 半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止,则在此过程中,下列说法正确的是( )
半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止,则在此过程中,下列说法正确的是( )| A. | MN对Q的弹力逐渐减小 | B. | P对Q的弹力逐渐增大 | ||
| C. | 地面对P的摩擦力逐渐减小 | D. | Q所受的合力逐渐增大 |
14.在“验证机械能守恒定律”的实验中不需测量或计算的物理量是( )
| A. | 下落高度 | B. | 瞬时速度 | C. | 重物质量 | D. | 时间 |
11.汽车由静止开始做加速度为a的匀加速运动,则汽车达到额定功率时,汽车的速度( )
| A. | 同时达到最大 | |
| B. | 还没有达到最大值 | |
| C. | 在没有达到额定功率前已经达到最大值 | |
| D. | 将在以后的过程中保持不变 |
 一列横波沿x轴方向传播,在t1=0时刻的波形图如图中实线所示,在t2=1s时刻的波形如图中的虚线所示,求:
一列横波沿x轴方向传播,在t1=0时刻的波形图如图中实线所示,在t2=1s时刻的波形如图中的虚线所示,求: 如图所示,高二10班物理研究性小组完成了以下两个演示实验,请你根据所学知识回答下列问题.
如图所示,高二10班物理研究性小组完成了以下两个演示实验,请你根据所学知识回答下列问题.