题目内容
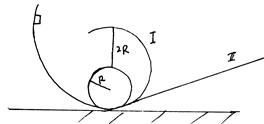
两根长直轨道与一半径为R的半圆型圆弧轨道相接于A、C两点，B点为轨道最低点，O为圆心，轨道各处光滑且固定在竖直平面内。质量均为m的两小环P、Q用长为R的轻杆连接在一起，套在轨道上。将MN两环从距离地面2R处由静止释放，整个过程中轻杆和轨道始终不接触，重力加速度为g，求：
（1）当P环运动到B点时，系统减少的重力势能△EP；
（2）当P环运动到B点时的速度v；
（3）在运动过程中，P环能达到的最大速度vm；
（4）若将杆换成长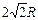
，P环仍从原处由静止释放，经过半圆型底部再次上升后，P环能达到的最大高度H。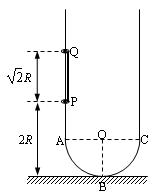
（1）当P环运动到B点时，系统减少的重力势能△EP；
（2）当P环运动到B点时的速度v；
（3）在运动过程中，P环能达到的最大速度vm；
（4）若将杆换成长
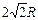，P环仍从原处由静止释放，经过半圆型底部再次上升后，P环能达到的最大高度H。（1）
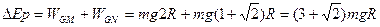
（2）AB都进入圆轨道后，两环具有相同角速度，则两环速度大小一定相等（或通过速度分解得到两环速度大小相同）
整体动能定理（或机械能守恒）：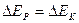
→
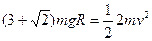
得到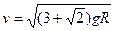
（3）当系统质心下降到最低处时，系统达到的速度最大，此时MN离O点竖直高度为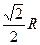
→
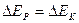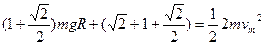
得到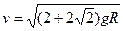
（4）由于杆超过了半圆直径， M再次上升后，设位置比原来高h。
由动能定理（或机械能守恒）：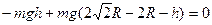
解得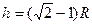
， M能达到的最大高度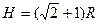
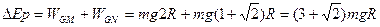
（2）AB都进入圆轨道后，两环具有相同角速度，则两环速度大小一定相等（或通过速度分解得到两环速度大小相同）
整体动能定理（或机械能守恒）：
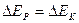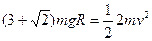
→得到
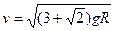
（3）当系统质心下降到最低处时，系统达到的速度最大，此时MN离O点竖直高度为
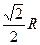
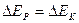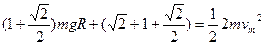
→得到
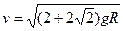
（4）由于杆超过了半圆直径， M再次上升后，设位置比原来高h。
由动能定理（或机械能守恒）：
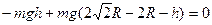
解得
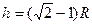， M能达到的最大高度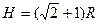略
练习册系列答案
阅读快车系列答案
相关题目
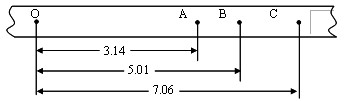
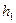。假设第二次重复第一的运动仍从半径为R的圆形轨道的最低端进入另一光滑平直斜面轨道II，轨道足够长，能上升的最大高度为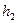
用><=表示）
