题目内容
15.如图,说法正确的是( )
| A. | 物体在第2s内的位移是4m | B. | 物体在第6s内的位移是4m | ||
| C. | 物体前6s内的位移是4m | D. | 物体后6s内的位移是4m |
分析 s-t图象的纵坐标表示物体某时刻的位置坐标,位移等于s的变化量,根据初、末位置的坐标分析物体的位移.
解答 解:A、物体在第2s内的位移是△s=s2-s1=4m-2m=2m,故A错误.
B、物体在第6s内的位移是△s=s2-s1=4m-4m=0m,故B错误.
C、物体在前6s内的位移是△s=s2-s1=4m-0m=4m,故C正确.
D、物体在后6s内的位移是△s=s2-s1=8m-4m=4m,故D正确.
故选:CD
点评 解决本题的关键要理解位移时间图象中点代表物体的位置,位移等于纵坐标的变化量.

练习册系列答案
相关题目
6.下列说法中正确的是( )
| A. | 研究地球自转时,可以把地球看成质点 | |
| B. | “地球围绕太阳转”,是以地球为参考系 | |
| C. | “第3秒初”就是第2秒末,指的是时刻 | |
| D. | 若物体运动路程不为零,则位移也不可能为零 |
10. 如图,有一矩形区域,水平边长为S=$\sqrt{3}$m,竖直边长为h=1m.质量均为m、带电量分别为+q和-q的两粒子,$\frac{q}{m}$=0.10C/kg.当矩形区域只存在场强大小为E=10N/C、方向竖直向下的匀强电场时,+q由a点沿ab方向以速率v0进入矩形区域,轨迹如图.当矩形区域只存在匀强磁场时,-q由c点沿cd方向以同样的速率v0进入矩形区域,轨迹如图.不计重力,已知两粒子轨迹均恰好通过矩形区域的几何中心.则( )
如图,有一矩形区域,水平边长为S=$\sqrt{3}$m,竖直边长为h=1m.质量均为m、带电量分别为+q和-q的两粒子,$\frac{q}{m}$=0.10C/kg.当矩形区域只存在场强大小为E=10N/C、方向竖直向下的匀强电场时,+q由a点沿ab方向以速率v0进入矩形区域,轨迹如图.当矩形区域只存在匀强磁场时,-q由c点沿cd方向以同样的速率v0进入矩形区域,轨迹如图.不计重力,已知两粒子轨迹均恰好通过矩形区域的几何中心.则( )
 如图,有一矩形区域,水平边长为S=$\sqrt{3}$m,竖直边长为h=1m.质量均为m、带电量分别为+q和-q的两粒子,$\frac{q}{m}$=0.10C/kg.当矩形区域只存在场强大小为E=10N/C、方向竖直向下的匀强电场时,+q由a点沿ab方向以速率v0进入矩形区域,轨迹如图.当矩形区域只存在匀强磁场时,-q由c点沿cd方向以同样的速率v0进入矩形区域,轨迹如图.不计重力,已知两粒子轨迹均恰好通过矩形区域的几何中心.则( )
如图,有一矩形区域,水平边长为S=$\sqrt{3}$m,竖直边长为h=1m.质量均为m、带电量分别为+q和-q的两粒子,$\frac{q}{m}$=0.10C/kg.当矩形区域只存在场强大小为E=10N/C、方向竖直向下的匀强电场时,+q由a点沿ab方向以速率v0进入矩形区域,轨迹如图.当矩形区域只存在匀强磁场时,-q由c点沿cd方向以同样的速率v0进入矩形区域,轨迹如图.不计重力,已知两粒子轨迹均恰好通过矩形区域的几何中心.则( )| A. | 磁场方向垂直纸面向外 | |
| B. | 两粒子各自离开矩形区域时的动能相等 | |
| C. | 由题给数据,初速度可求 | |
| D. | 由题给数据,磁感应强度可求 |
7.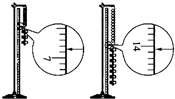 某同学和你一起探究弹力和弹簧伸长量的关系,并测弹簧的劲度系数k,做法是:先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上,当弹簧自然下垂时,指针指示的刻度数值记为L0;弹簧下端挂一个50g的钩码时,指针指示的刻度数值记为L1;弹簧下端挂两个50g的钩码时,指针指示的刻度数值记为L2…弹簧下端挂七个50g的钩码时,指针指示的刻度数值记为L7.
某同学和你一起探究弹力和弹簧伸长量的关系,并测弹簧的劲度系数k,做法是:先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上,当弹簧自然下垂时,指针指示的刻度数值记为L0;弹簧下端挂一个50g的钩码时,指针指示的刻度数值记为L1;弹簧下端挂两个50g的钩码时,指针指示的刻度数值记为L2…弹簧下端挂七个50g的钩码时,指针指示的刻度数值记为L7.
(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.
测量记录表:
(2)实验中,L3和L7两个值还没有测定,请你根据下图将这两个测量值填入记录表中.
(3)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm.请你给出第四个差值d4=L7-L3=7.20cm
(4)根据以上差值,可以求出每增加50g钩码弹簧的平均伸长量△L.△L用d1、d2、d3、d4表示的式子为△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{4×4}$,代入数据解得△L=1.75cm.
(5)计算弹簧的劲度系数k=28N/m.
 某同学和你一起探究弹力和弹簧伸长量的关系,并测弹簧的劲度系数k,做法是:先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上,当弹簧自然下垂时,指针指示的刻度数值记为L0;弹簧下端挂一个50g的钩码时,指针指示的刻度数值记为L1;弹簧下端挂两个50g的钩码时,指针指示的刻度数值记为L2…弹簧下端挂七个50g的钩码时,指针指示的刻度数值记为L7.
某同学和你一起探究弹力和弹簧伸长量的关系,并测弹簧的劲度系数k,做法是:先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上,当弹簧自然下垂时,指针指示的刻度数值记为L0;弹簧下端挂一个50g的钩码时,指针指示的刻度数值记为L1;弹簧下端挂两个50g的钩码时,指针指示的刻度数值记为L2…弹簧下端挂七个50g的钩码时,指针指示的刻度数值记为L7.(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.
测量记录表:
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 6.85 | 8.60 | 10.3 | 12.1 | 14.05 |
(3)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm.请你给出第四个差值d4=L7-L3=7.20cm
(4)根据以上差值,可以求出每增加50g钩码弹簧的平均伸长量△L.△L用d1、d2、d3、d4表示的式子为△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{4×4}$,代入数据解得△L=1.75cm.
(5)计算弹簧的劲度系数k=28N/m.
8.如图甲所示,质量为2kg的物体在与水平方向成37°角斜向下的恒定推力F作用下沿粗糙的水平面运动,1s后撤掉推力F,其运动的v-t图象如图乙所示.(sin37°=0.6,cos37°=0.8,g=10m/s2)下列说法错误的是( )


| A. | 在0.5s时,推力F的瞬时功率为300W | |
| B. | 在0~2s内,合外力一直做正功 | |
| C. | 在0~2s内,合外力的平均功率为12.5W | |
| D. | 在0~3s内,物体克服摩擦力做功为120J |

 如图所示,线圈A通过滑动变阻器和开关连接到直流电源上,线圈B两端连接到电流表上,把线圈A装在线圈B的里面,合上开关.当滑动变阻器的滑片保持不动时电流表的指针不偏转(填“偏转”或“不偏转”);当滑动变阻器的滑片快速滑动时电流表的指针偏转(填“偏转”或“不偏转”).
如图所示,线圈A通过滑动变阻器和开关连接到直流电源上,线圈B两端连接到电流表上,把线圈A装在线圈B的里面,合上开关.当滑动变阻器的滑片保持不动时电流表的指针不偏转(填“偏转”或“不偏转”);当滑动变阻器的滑片快速滑动时电流表的指针偏转(填“偏转”或“不偏转”).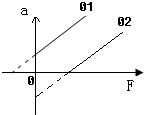 在“研究加速度与力的关系”的实验中:
在“研究加速度与力的关系”的实验中: