题目内容
A、B两个小物块用轻绳连结，绳跨过位于倾角为300的光滑斜面顶端的轻滑轮，滑轮与转轴之间的摩擦不计，斜面固定在水平桌面上，如图甲所示．第一次， A悬空，B放在斜面上，用t表示B自斜面底端由静止开始运动至斜面顶端所需的时间．第二次，将A和B位置互换，使B悬空，A放在斜面上，发现A自斜面底端由静止开始运动至斜面顶端所需的时间为t/2．（重力加速度g已知）
（1）求A与B两小物块的质量之比．
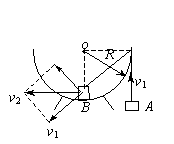
（2）若将光滑斜面换成一个半径为R（已知）的半圆形光滑轨道固定在水平桌面上，将这两个小物块用轻绳连结后，如图放置，现将B球从轨道边缘由静止释放．若不计一切摩擦，求：B沿半圆形光滑轨道滑到底端时，A、B的速度大小．
（1）
（2）
解析:
（1）设A的质量为m1、B的质量为m2
第一次，A悬空，B放在斜面上，将A、B看成整体，由牛顿第二定律有
设斜面的长度为L，依题意有 
第二次，将A和B位置互换，使B悬空，A放在斜面上，同理有
由以上4式得到
（2）光滑斜面换成一个半径为R的半圆形光滑轨道时，Ｂ球从轨道边缘由静止释放后到达轨道底端时速度为v2，此时Ａ的速度为v1，如图所示．
由动能定理有 
由速度关系有 
解得：
练习册系列答案
相关题目
A、B两个小物块用轻绳连结，绳跨过位于倾角为30°的光滑斜面（斜面足够长）顶端的轻质滑轮，滑轮与转轴之间的摩擦不计，斜面固定在水平桌面上，如图所示．第一次，B悬空，A放在斜面上，A恰好静止；第二次，将B的质量改变，发现A自斜面顶端由静止开始运动，经时间t速度大小为v，已知物块A的质量为m，重力加速度为g，求物块B质量改变了多少？
（2011?河南模拟）A、B两个小物块用轻绳连接，绳跨过位于倾角为30°的光滑斜面顶端的轻滑轮，滑轮与转轴之间的摩擦不计，斜面固定在水平桌面上，如图所示．第一次，A悬空，B放在斜面上，B自斜面底端由静止开始运动至斜面顶端所需的时间为t．第二次，将A和B位置互换，使B悬空，A放在斜面上，发现A自斜面底端由静止开始运动至斜面顶端所需的时间为
如图甲所示，质量分别为m=1kg，M=2kg的A、B两个小物块用轻弹簧相连而静止在光滑水平面上，在A的左侧某处另有一个质量也为m=1kg的小物块C以V0=4m/s的速度正对A向右匀速运动，一旦与A接触就将粘合在一起运动，若在C与A接触前，使A获得一初速度VA0，并从此时刻开始计时，向右为正方向，其速度随时间变化的图象如图乙所示（C与A未接触前），弹簧始终未超过弹簧性限度．
，求A与B两小物块的质量之比。
